分類
Table of Contents
1. 關於分類(Classification)
當我們在做分類任務時,其實就是想讓電腦幫我們「把資料分對類別」,就像圖中這個常見的例子 —— 判斷一封 Email 是不是垃圾郵件(見 圖1)。這個任務的目標是將一封 Email 分為兩類:垃圾郵件或非垃圾郵件。
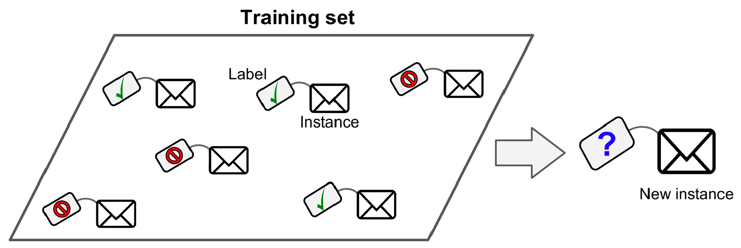
Figure 1: 典型的監督式學習:垃圾郵件分類
這個任務的目標是將一封 Email 分為兩類:垃圾郵件或非垃圾郵件。為了達成這個目標,我們需要先收集一些特徵值(如:Email 的主題、內容、發件人等),然後利用這些特徵值來訓練一個分類器,最後用這個分類器來預測新的 Email 是屬於哪一類。
分類是監督式學習的方法之一(另一種為迴歸),分類問題也稱為離散(discrete)預測問題,因為每個分類都是一個離散群組。In supervised learning, the training set you feed to the algorithm includes the desired solutions, called labels1.
分類可以再細分為兩類:
- Binary Classification(二元分類)
就是「這是 or 不是」的判斷,例如:
- 垃圾信 vs. 正常信
- 有病 vs. 沒病
- 是狗 vs. 不是狗
- Multiclass Classification(多類別分類)
當資料有三種以上的分類,例如:
- 判斷一張圖片是狗、貓還是鳥
- 分辨手寫數字是 0~9 中的哪一個
實務上常見的分類演算法有:
- 最短距離分類器: 看你離哪一類的「代表點」最近,就歸到那一類。直覺又快速。
- KNN 分類器(K 最近鄰): 看你附近的 K 個鄰居是屬於哪一類,跟著他們一起歸類。這就像「看你周圍的人在看什麼影片,猜你也喜歡那類型」。
- 決策樹(Decision Tree): 一層一層問問題做判斷,像是「如果這封信有 ’買一送一’ 就走左邊,有就走右邊」,最後走到一個葉節點來決定類別。
這些分類方法,就是我們在做監督式學習時常會用到的工具。讓電腦透過「已知答案的資料」學會怎麼幫我們分辨新資料的類別。
2. 最短距離分類器
這種方法的核心觀念很簡單:把新來的資料和已知資料做比較,看看「距離哪一類最近」,就判斷它是屬於那一類。
換句話說,就是用「特徵距離」來量資料彼此的相似度:
- 距離近 → 類似度高
- 距離遠 → 類似度低
這就像英文裡常說的那句話:
Birds of the same kind are often seen to flock and fly together. (物以類聚,近者為群。)
2.1. 任務: 分辨貓狗
現在我們要訓練一個分類器,幫我們判斷圖片是貓還是狗。
操作流程:
- 我們先蒐集一些已知的訓練資料(例如標記好的貓圖和狗圖)
- 對每張圖提取特徵(可能是耳朵長度、眼睛距離、毛色紋理等等)
- 接著對於一張新進來的圖片,就:
- 把它的特徵拿來和資料庫裡的資料做比對
- 算算看它「離誰最近」
- 就把這張新圖歸到那個類別
- 如果它離「狗圖」比較近,就預測它是狗;離「貓圖」比較近,就預測它是貓。

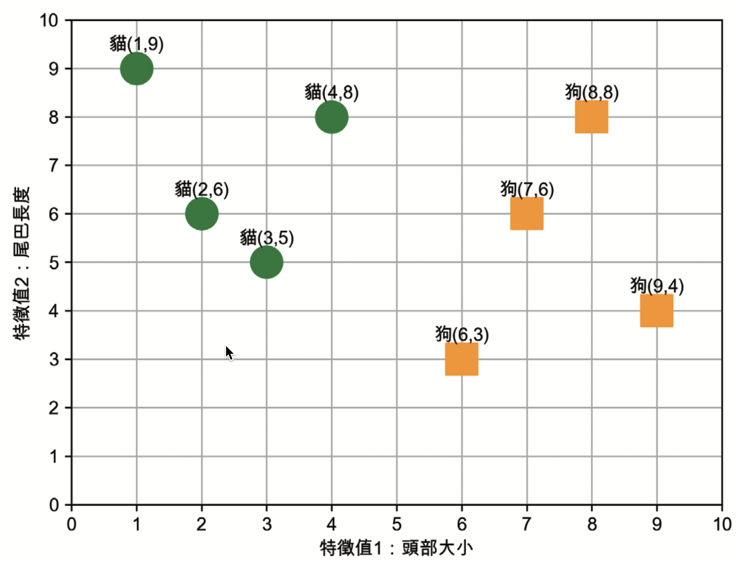
Figure 2: 貓與狗的外觀比較
假設貓與狗在外觀上較明顯的區別(特徵)為頭部大小及尾巴長度,其中:
- 頭部大小:計算圖中動物的頭部與身體比例,將比例值分為 10 個類別,比例值越高,代表頭部所佔面積越大。
- 尾巴長度:計算圖中動物尾巴與身體長度比例,將比例值分為 10 個類別,比例值越高,代表尾巴越長。
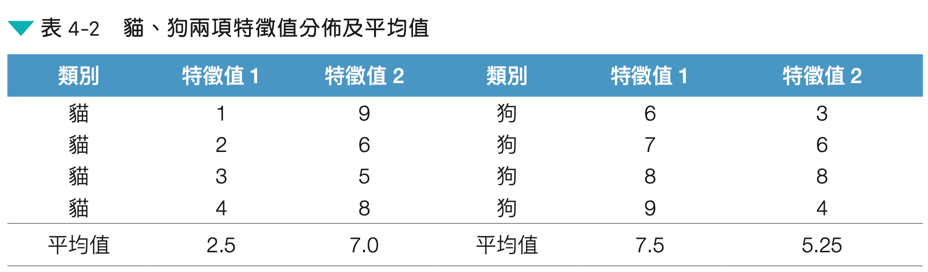
這個資料集裡有 8 張照片,其中兩張為:

Figure 3: 資料集範例
問題:如果出現了一張新動物的圖片,在測量出這張新照片中動物的特徵值後,我們如何利用現有的這 8 張圖的訓練資料來判斷新圖裡的動物是貓還是狗?
2.2. 最短距離分類器工作原理
2.2.2. 對新資料預測
現在我們可以對新資料進行預測,如果有一張新圖被送進模型,其兩項特徵值為(頭部大小 5,尾巴長度 6)(如圖6中的▲),那這張圖比較可能是貓還是狗呢?
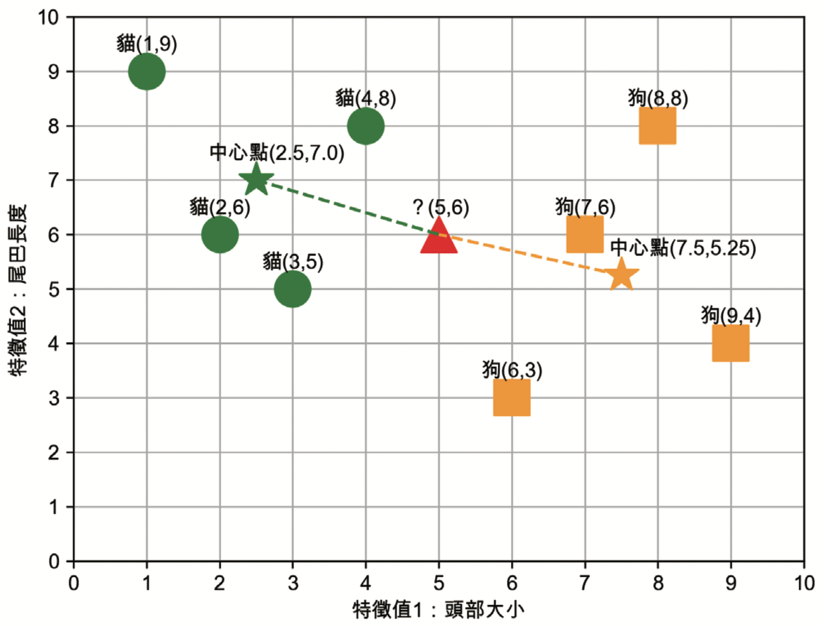
Figure 6: 比較新資料與兩個中心點的距離
最短距離法的判斷方式是:比較▲與兩個中心點(★與★)的直線距離(歐幾里德距離),也就是說,▲離哪個中心點直線距離較短就將之視為那種動物。計算方式如下:
- ▲與★的直線距離為 \( \sqrt{(5 − 2.5)^2 + (6 − 7.0)^2 } \approx 2.69 \)
- ▲與★的直線距離為 \( \sqrt{(5 − 7.5)^2 + (6 − 5.25)^2} \approx 2.61 \)
根據上述計算結果,▲離★較近,模型對這張新圖的預測結果為:狗。 上述範例是一個簡化的監督式學習模型工作原理,可預期當我們對於訓練資料掌握的特徵值越詳盡(如:對每張圖片建構出 1000 個特徵值),則預測結果應該也會越精確,但隨著訓練資料的增加(如:有 100 萬張訓練圖片),則整個運算量將會變得十分龐大。
2.3. 其他計算距離的方式
除了使用中心點做為距離判斷依據,也可以計算新進資料與 所有 資料集中各類資料點的距離,這裡的距離可以是曼哈頓距離或是歐幾里得距離。
2.4. [作業]手刻最短距離分類器 TNFSH
2.4.1. Numpy solution:
1: import numpy as np 2: 3: a = list(map(float, input().split())) 4: x, y = a[0], a[1] 5: 6: groupA = np.array([[4, 6], [5, 7], [5, 8], [5.8, 6], [6, 6], [6, 7], [7, 5], [7, 7], [8, 4], [9, 5]]) 7: groupB = np.array([[2, 2], [4, 2], [4, 4], [5, 4], [5, 3], [6, 2]]) 8: 9: # 計算兩組的中心點 10: xa, ya = np.mean(groupA, axis=0) 11: xb, yb = np.mean(groupB, axis=0) 12: 13: # 計算輸入點到兩組中心點的距離 14: distanceA = (xa - x) ** 2 + (ya - y) ** 2 15: distanceB = (xb - x) ** 2 + (yb - y) ** 2 16: 17: if distanceA > distanceB: 18: print('B') 19: else: 20: print('A')
3. KNN 分類器:IRIS
K-Nearest Neighbor 分類算法由 Cover 和 Hart 在 1968 年提出,想法是:如果一個樣本在特徵空間中的 k 個最相鄰的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別,並具有這個類別上樣本的特性。步驟如下:
- 選定 k 的值和一個「距離度量」(distance metric)。
- 找出 k 個想要分類的、最相近的鄰近樣本。
- 以多數決的方式指定類別標籤。
3.1. [實作]鳶尾花分類 sklearn
3.1.1. DataSet
收集了 3 種鳶尾花的四個特徵,分別是花萼(sepal)長度、寬度、花瓣(petal)長度、寬度,以及對應的鳶尾花種類。這四個特徵值組成了我們的輸入特徵(features),而花的種類則是我們要分類的標籤(label)。

Figure 7: 鳶尾花的花萼與花瓣
3.1.1.1. 關於Iris資料集作者: Fisher
這份著名的 Iris 鳶尾花資料集,最早由英國統計學家 羅納德·費雪(Sir Ronald Aylmer Fisher) 在研究中提出。 他不只是統計學界的傳奇人物,也是演化生物學與遺傳學的重要奠基者之一。
美國歷史學家 Anders Hald 曾稱他為:
「幾乎以一人之力建立現代統計科學的天才」
理查·道金斯更直接讚譽他為:
「達爾文最偉大的繼承者」

Figure 8: Sir R.A. Fisher
Iris資料集是 Sir R.A. Fisher 在 1936 年發表的論文中首次介紹的,並且在統計學和機器學習領域廣泛使用。關於這個資料集有個有趣的小知識:R 語言的 iris 資料集與 Fisher 論文版本一致,但 UCI ML Repository 有兩筆資料是錯的。
- Fisher 的學術成就
- 共變數分析(ANCOVA)
- 最大概似估計法(Maximum Likelihood Estimation)
- 提出 p 值概念 與「0.05 顯著水準」(即 20 次實驗中有 1 次發生)為統計顯著性的臨界值,並應用於基於常態分布的雙尾檢定而形成日後所謂「兩個標準差法則」2。
- 實驗設計法(Design of Experiments)
- 被譽為「現代統計學之父」
3.1.1.2. 紅茶與牛奶的傳奇實驗3

Figure 9: Tea time
- 時間: 1920 年代的劍橋大學,某個風和日麗的夏天下午,一群人優閒地享受下午茶時光。
- 起因: 有位女士(生物學家 Muriel Bristol4)聲稱:「沖泡的順序對於奶茶的風味影響很大,把茶加進牛奶裡和把牛奶加進茶裡,這兩種沖泡方式所泡出的奶茶口味截然不同。」,而且她有能嚐出二者差異的超能力。
Fisher 說: 林北聽妳在唬爛(That’s impossible.)

Figure 10: Muriel Bristol
- 推手: 化學家 William Roach 為了拍 Muriel Bristol 馬屁,建議做個實驗
- 結果: Fisher 利用這個實驗的結果,正式發展出了:實驗設計原理與統計假設檢定框架,現代統計學就此誕生。
- 問題: 如果你是 Fisher,你要怎麼證明 Bristol 是對的或錯的? 實際泡茶? 怎麼泡? 要泡幾杯、讓 Bristol 猜幾杯才能確定 Bristol 的超能力。
3.1.2. 模型任務
輸入花萼和花瓣資料後,推測所屬的鳶尾花類型。

Figure 11: 三種鳶尾花
3.1.3. 實作
3.1.3.1. 讀取資料集
1: from sklearn import datasets 2: # 讀入資料 3: iris = datasets.load_iris() 4: print(iris.DESCR)
3.1.3.2. 取出特徵與標籤
1: from sklearn import datasets 2: 3: # 讀入資料 4: iris = datasets.load_iris() 5: 6: x = iris.data 7: y = iris.target 8: print(x[:5]) 9: print(y[:5])
[[5.1 3.5 1.4 0.2] [4.9 3. 1.4 0.2] [4.7 3.2 1.3 0.2] [4.6 3.1 1.5 0.2] [5. 3.6 1.4 0.2]] [0 0 0 0 0]
3.1.3.3. 資料觀察
先將資料視覺化,有助於我們對於資料分佈與預測結果先有一個概念。為了方便以二維圖形呈現結果,我們先隨意挑兩個特徵值來觀察一下。
1: import matplotlib.pyplot as plt 2: import pandas as pd 3: import seaborn as sns 4: from sklearn import datasets 5: 6: # 讀入資料 7: iris = datasets.load_iris() 8: 9: x = iris.data 10: y = iris.target 11: 12: #把nupmy ndarray轉為pandas dataFrame,加上columns title 13: npx = pd.DataFrame(x, columns=['fac1','fac2','fac3','fac4']) 14: npy = pd.DataFrame(y.astype(int), columns=['category']) 15: #合併 16: dataPD = pd.concat([npx, npy], axis=1) 17: print(dataPD) 18: # 畫圖 19: sns.lmplot(x='fac1', y='fac2', data=dataPD, hue='category', fit_reg=True) 20: plt.savefig('images/irisdemo.png', dpi=300)
fac1 fac2 fac3 fac4 category
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0
.. ... ... ... ... ...
145 6.7 3.0 5.2 2.3 2
146 6.3 2.5 5.0 1.9 2
147 6.5 3.0 5.2 2.0 2
148 6.2 3.4 5.4 2.3 2
149 5.9 3.0 5.1 1.8 2
[150 rows x 5 columns]
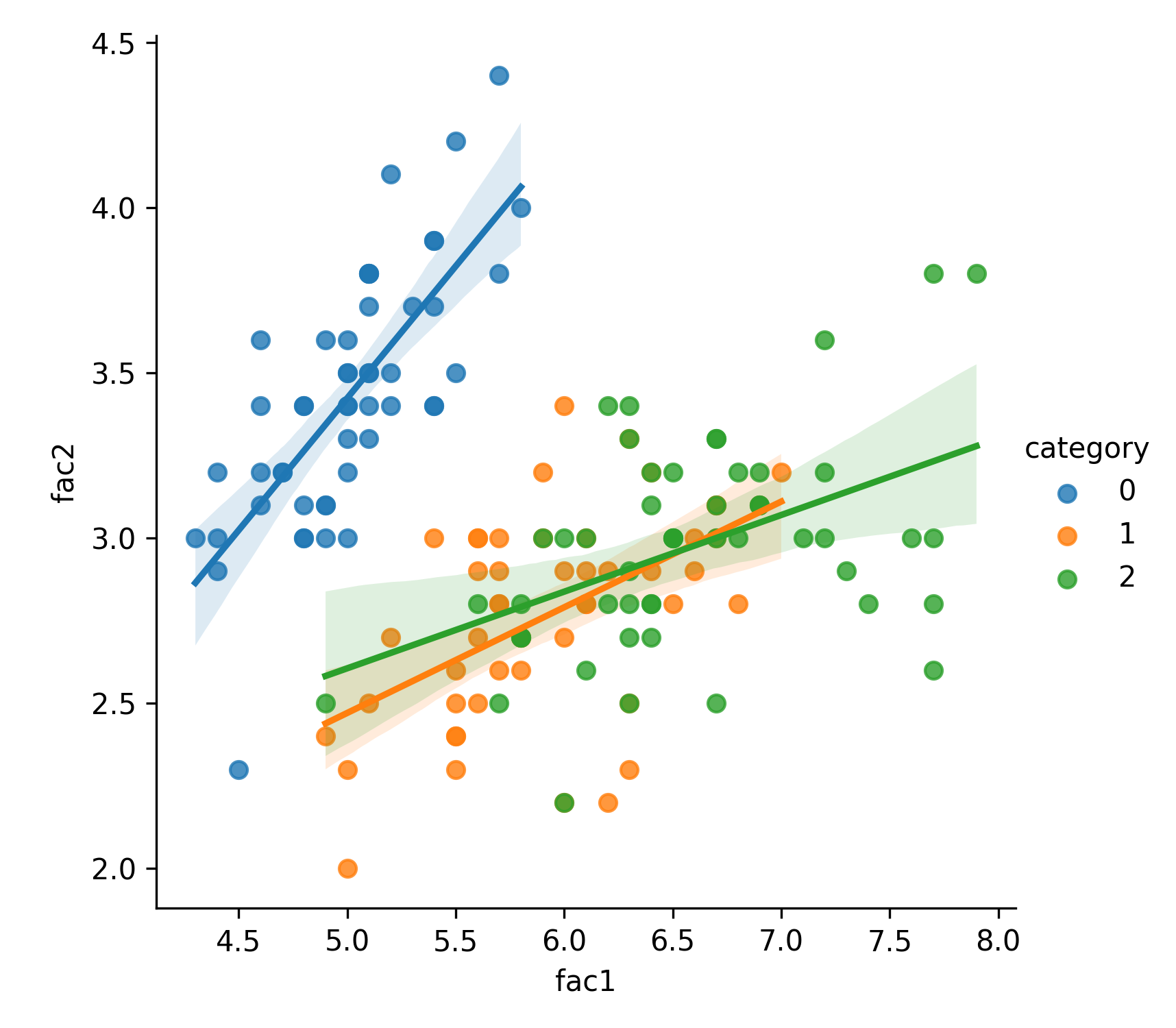
Figure 12: Iris 不同特徵值與其類別的關係
3.1.3.4. 分割資料集
在訓練模型之前,我們通常會把資料集隨機分成訓練集和測試集,這樣才能公平地評估模型預測新資料的能力。
Scikit-learn 提供了很方便的工具:train_test_split(),import方式如下:
1: from sklearn.model_selection import train_test_split 2: # 劃分資料集 3: x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=6)
train_test_split()這個函式的特色:
- 一行就能完成切分,會自動幫我們打亂順序、對齊 X 和 y
- 本質上是把以下流程包起來:
- 驗證輸入資料格式
- 使用隨機抽樣(例如 ShuffleSplit)
- 回傳對應切分後的訓練與測試資料
train_test_split()接受三個參數:原始的資料、Seed、比例
- 原始的資料:就如同上方的 data 一般,是我們打算切成 Training data 以及 Test data 的原始資料
- Seed: 亂數種子,可以固定我們切割資料的結果
- 比例:可以設定 train_size 或 test_size,只要設定一邊即可,範圍在 [0-1] 之間
- 官網: sklearn.model_selection.train_test_split
3.1.3.5. 資料標準化
為了讓模型更好地學習特徵值之間的關係,我們需要對資料進行標準化處理。這樣可以使每個特徵值的均值為 0,標準差為 1,從而提高模型的收斂速度和預測準確性。
此處利用 preprocessing 模組裡的 StandardScaler 類別將資料標準化
1: from sklearn.preprocessing import StandardScaler 2: # 利用fit方法,對X_train中每個特徵值估平均數和標準差 3: # 然後對每個特徵值進行標準化(train和test都要做) 4: # 特徵工程:標準化 5: transfer = StandardScaler() 6: x_train = transfer.fit_transform(x_train) 7: x_test = transfer.transform(x_test)
3.1.3.6. 訓練、評估模型效能
- 測試一下 k=2 的效能
- 以訓練集來訓練模型,然後以測試集來評估模型的準確性
1: from sklearn.neighbors import KNeighborsClassifier 2: # KNN 分類器 3: estimator = KNeighborsClassifier(n_neighbors=2) 4: estimator.fit(x_train, y_train) 5: 6: # 模型評估 7: # 方法一:直接對比真實值和預測值 8: y_predict = estimator.predict(x_test) 9: print('y_predict:\n', y_predict) 10: print('直接對比真實值和預測值:\n', y_test == y_predict) 11: 12: # 方法二:計算準確率 13: score = estimator.score(x_test, y_test) 14: print('準確率:\n', score)
y_predict: [0 2 0 0 2 1 1 0 2 1 1 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1 2] 直接對比真實值和預測值: [ True True True True True True False True True True False True True True True False True True True True True True True True True True True True True True True True True True False True True True] 準確率: 0.8947368421052632
3.1.4. 關於得分
- estimator.score()是用來計算模型在測試數據上的準確率,表示模型預測正確的比例,取值範圍在 0 到 1 之間。
- 一般來說,0.7(70%) 以上的準確率就算是不錯,但具體標準取決於任務難度和數據集特性。
- 如果數據集不平衡(例如,某個類別佔了大多數),即使高於 0.7 也可能不一定是好結果,這時需要結合其他指標如精確率(Precision)或召回率(Recall)來評估模型。
3.2. [作業]手刻 KNN 分類器 TNFSH
3.3. [作業]分析 K 值對模型效能的影響 TNFSH
修改 KNN 分類器:IRIS 程式碼,完成以下任務
- 以不同的 K 值進行 KNN 預測
- 以折線圖表示 K 值與 KNN 預測準確度間的關係
- 哪一種 K 值的預測準確度最高?請自行想辦法在圖上標示出準確度最高的 K 值
4. 決策樹分類器
「決策樹(Decision Tree)」是一種條件式的分類器,可以想像成一個不斷問問題、分資料的樹狀結構,非常適合用來處理分類問題。整體的建構方式是由上而下,每次根據一個特徵做出選擇,逐步把資料分得越來越細。
Figure 13: 一棵複雜的決策樹
4.1. 決策樹運作流程
- 從整個資料集開始,先挑出一個最能區分資料的特徵(例如:花瓣長度)
- 依據這個特徵的值,把資料分成兩群或多群(像是「大於 2.5 公分的分一邊,其它分一邊」)
- 對每一群資料再重複這個動作:挑新的特徵再往下切
- 這樣一直切、一直分,直到每一群資料裡面只剩下同一個類別,就不再繼續往下分了,這就是「葉節點」
4.1.1. 一個簡單的決策樹範例: XXX, 出來打球
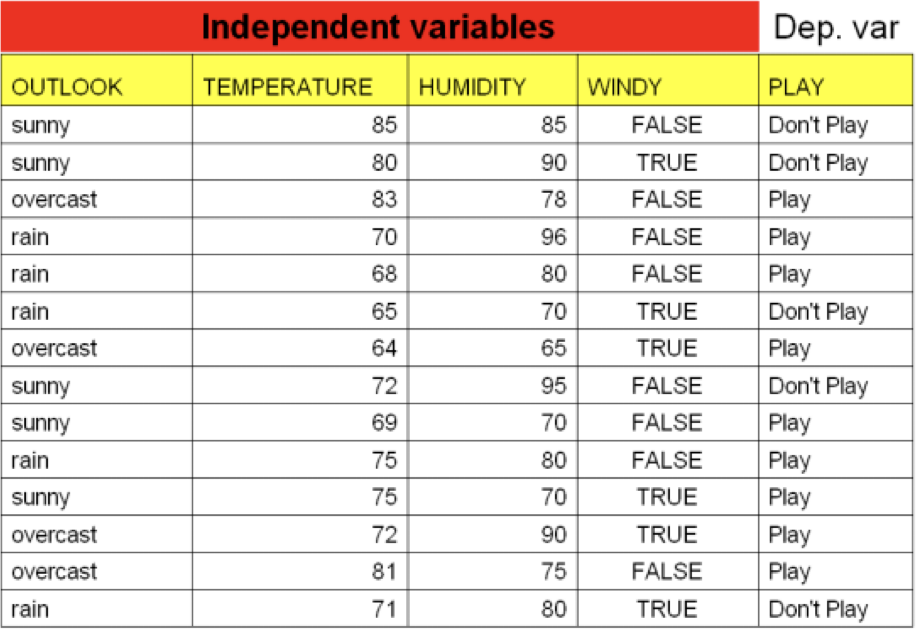
Figure 14: 影響打球的天候因素
圖14為某間高爾夫俱樂部決定是否開放球場的因素,包括:
- outlook:天象
- overcast:陰天
- humidity:濕度
- windy:颳風
如何建立一個決策系統來協助業者自動判斷?我們可以建立一棵如下的決策樹:
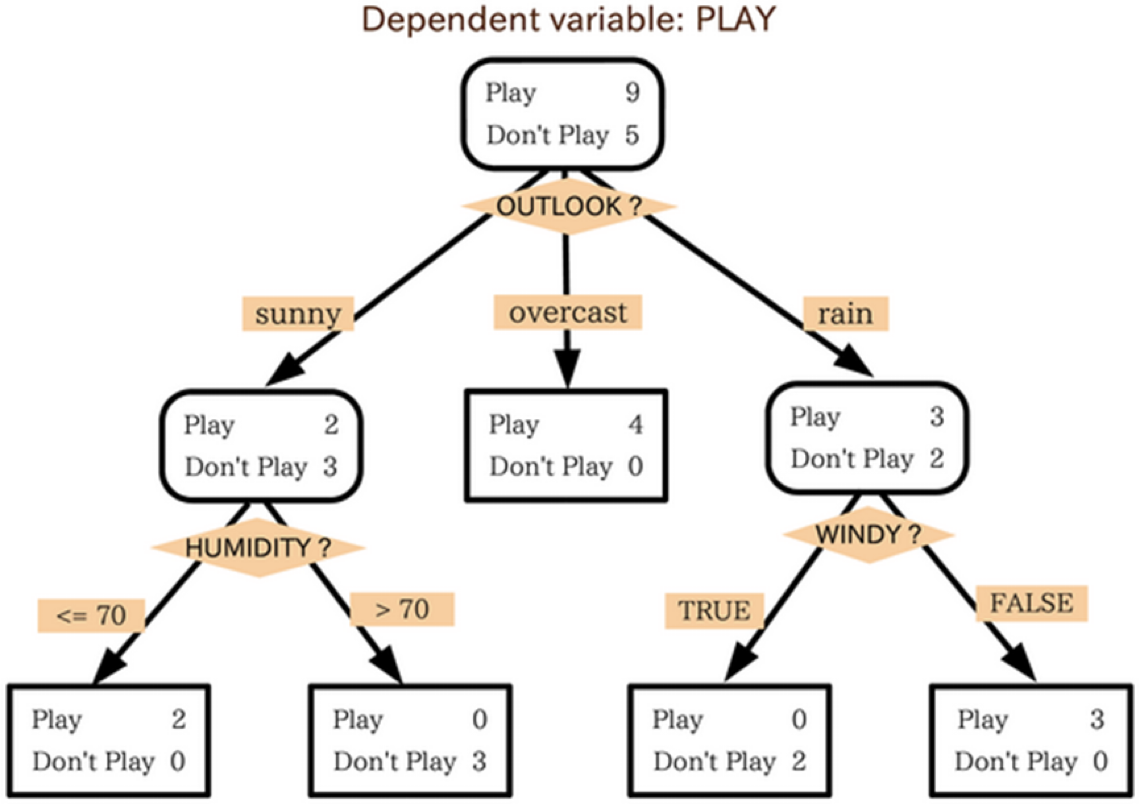
Figure 15: 目標決策樹
4.2. [實作]誰會買筆電:
現在就讓我們化身為 3C 賣場的員工,針對消費者是否購買筆記型電腦的消費記錄來建構出一棵決策樹吧!
| 年紀 | 收入 | 學生與否 | 購買筆電與否 |
|---|---|---|---|
| <=30 | 高 | 否 | 否 |
| 31…40 | 高 | 否 | 是 |
| >40 | 中 | 否 | 是 |
| >40 | 低 | 是 | 否 |
| 31…40 | 低 | 是 | 是 |
| <=30 | 中 | 否 | 否 |
| <=30 | 低 | 是 | 是 |
| <=30 | 中 | 是 | 是 |
| 31…40 | 中 | 否 | 是 |
| 31…40 | 高 | 是 | 是 |
| >40 | 中 | 是 | 否 |
4.2.1. 第一步:決定要先用哪一項特徵值
依據「是否購買筆記型電腦」的結果,到底要用哪一個特徵值來當成樹根?
- 年紀:<=30、30…40、>=40。
- 收入:低、中、高。
- 學生與否:是、否。
4.2.1.1. 作法 1: 暴力解決
將每個特徵值都當作分類的條件一一去建構決策樹,彷彿以列舉的方式將 所有的特徵值 排列組合出很多的決策樹,再一一分析哪一種可以有「最好的分類結果」。
4.2.1.2. 作法 2: 優雅策略
希望越優先選擇的條件,越能有效率地將訓練資料較為明顯地分類成幾個類別,如此便能減少判斷條件的次數,也能讓決策樹較為精簡有效率。
數學上常用來定義分類優劣程度的指標
- Gini index
- Information Gain: Entropy
4.2.2. Gini Index
Gini Index 的實作演算法是 CART tree。CART 是 Classification And Regression Tree 的縮寫,因此兼具分類與迴歸兩種功能。
Gini Index 與 Information Gain 的差別:
- Information Gain:一次可產生多個不同節點,
- Gini Index:一次僅能產生兩個,即 True 或 False 的 Binary 的二元分類樹。
如下圖我們想從 30 位學生中找出有打板球 15 位學生,左圖用性別做區分右圖用班級做區分。很合理的猜測男生一定是比較喜歡運動用性別應該有不錯效果,而用班級區分除非有體育班否則兩分類結果應該雷同。
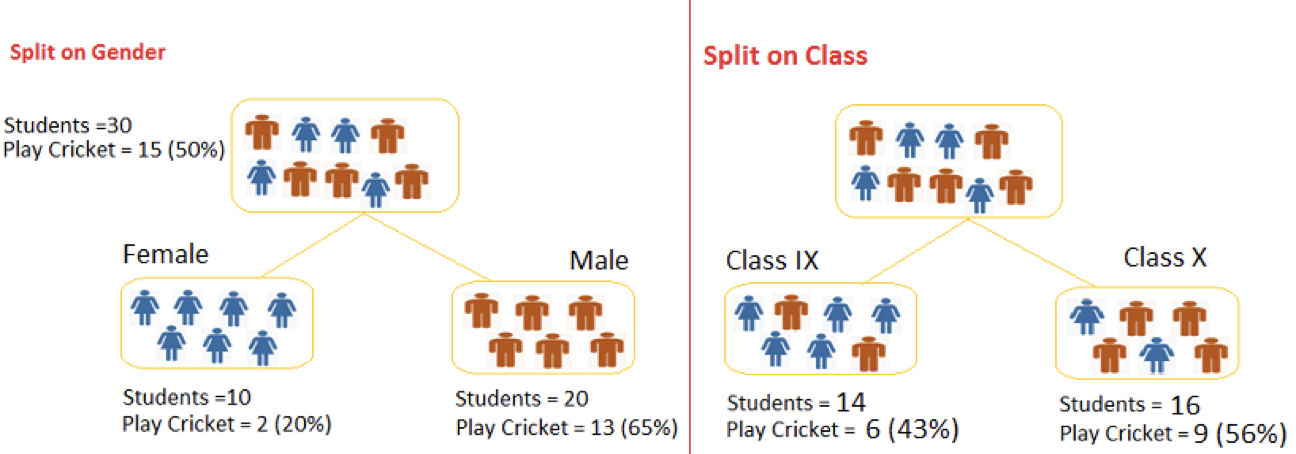
Figure 16: Gini Index
這兩種分法哪一種比較好?我們可以來算一算每一種分法的 Gini index。
- Gini 公式: \( Gini(S) = \sum\limits_{j=1}^{n}p^2_j \)
- 若依特徵值 A 分割資料集合 S 為 S1 與 S2,則計算式為: \( Gini_A(S) = \frac{|S_1|}{|S|}Gini(S_1)+\frac{|S_2|}{|S|}Gini(S_2) \)
4.2.2.1. 用性別分類(圖16左)
- Female 節點:10 位女性,其中有 2 位打板球 8 位不打,Gini 係數為 \((\frac{2}{10})^2+(\frac{8}{10})^2=0.68\)
- Male 節點:20 位男性,其中有 13 位打板球 7 位不打,Gini 係數為 \((\frac{13}{20})^2+(\frac{7}{20})^2=0.55\)
- 因此以性別分類的 Gini 係數加權後為:\(\frac{10}{30}*0.68+\frac{20}{30}*0.55=0.59\)
4.2.2.2. 用班級分類
- Class IX 節點:此班 14 位同學,其中 6 位打板球 8 位不打,因此 Gini 係數為 \((\frac{6}{14})^2+(\frac{8}{14})^2=0.51\)
- Class X 節點:此班 16 位同學,其中 9 位打板球 7 位不打,因此 Gini 係數為\((\frac{9}{16})^2+(\frac{7}{16})^2=0.51\)
因此以班級分類的決策樹,其 Gini 係數加權結果: \(\frac{14}{30}*0.51+\frac{16}{30}*0.51=0.51\)
4.2.2.3. 結果
兩樹相互比較(性別:0.59/班級:0.51)分類,因此系統會採用性別來進行節點的分類。
4.2.3. Entropy
熵(entropy)原本是物理學概念,代表事物的混亂程度:熵愈高、事物愈混亂。資訊理論(Information Theory)之父夏農(Claude Shannon)於 1948 年將熵引入電腦科學,成為代表資訊量的量度5,用來衡量一組資料的不確定性(uncertainty),因此又名為夏農熵(Shannon)。
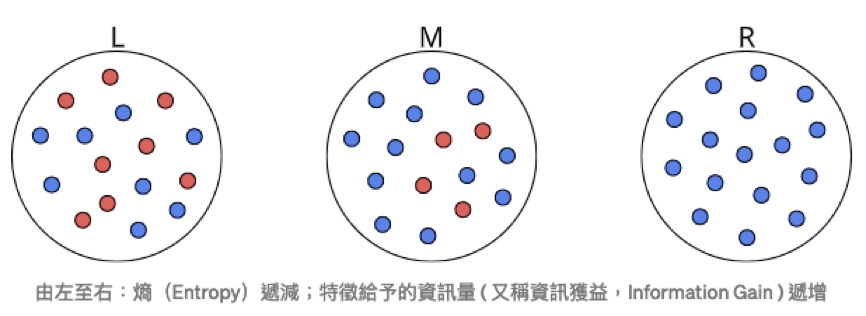
Figure 17: 幾種不同的熵值
資訊熵(information entropy)的概念也很簡單,就是熵愈高,資訊愈多。也就是愈混亂,資訊愈多5。
當所有資料的類型都是一致時,得到的熵為 0(如圖17右),但如果資料類型各自對半呈現差異時,熵為 1(如圖17左)。
另一種解讀 Entropy 的方式為將其視為度量資訊量的單位:
- 度量距離: cm/meter
- 度量時間: sec/min
- 度量資訊: 資訊量,資訊量指的是「如果我們要度量一個未知事物,那麼我們需要查詢的資訊有多少」,單位是位元。
再以丟硬幣為例:
- 1 枚硬幣 2 面都是人頭,結果確定,無不確定性,熵值為 0 。
- 1 枚正常硬幣,有 50%的機率猜中投擲結果,熵值為 1。
- 2 枚正常硬幣,有 33%的機率猜中其投擲結果(正正、反反、正反),不確定性>1 枚硬幣,其熵值約為 1.58 。
隨著不確定性增加,熵值也會增加。
4.2.3.1. 賭馬
- 機率相同
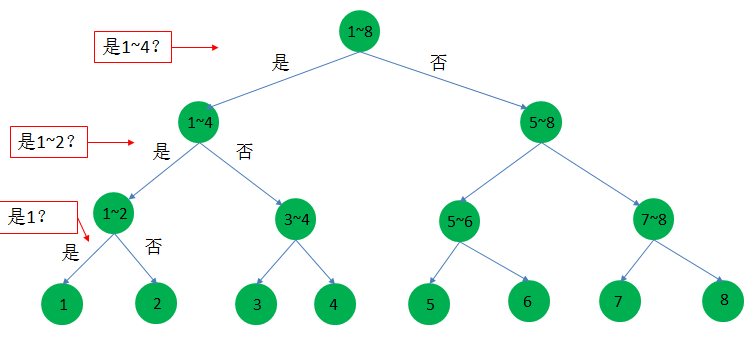
Figure 18: 機率相等下的熵
我們先假設每匹馬獲勝的機率都一樣,如圖18利用二分法,那麼只要猜測三次就可以找到所需資訊,需要的資訊量: 3 位元。
- 機率不同
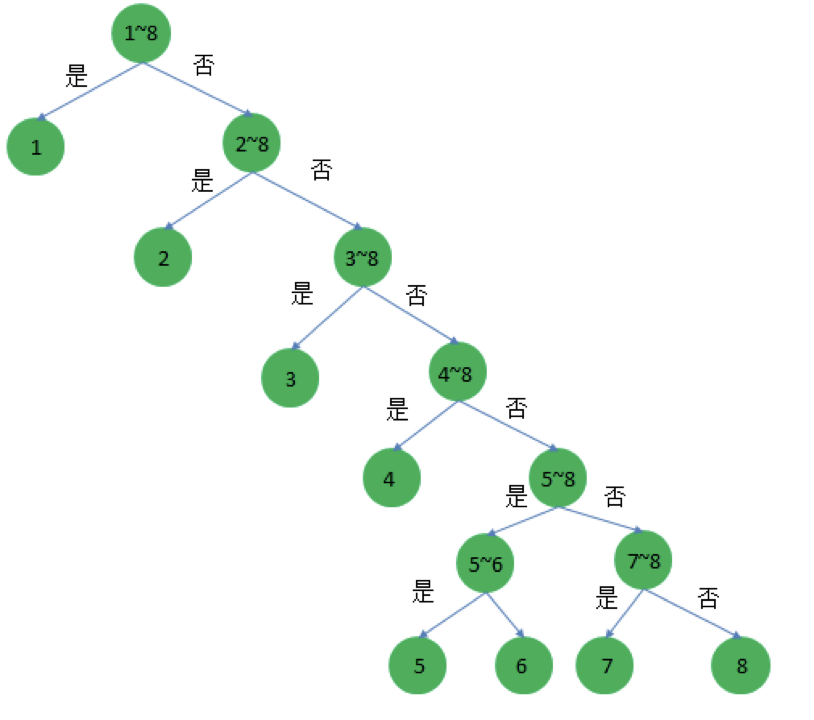
Figure 19: 機率不相等下的熵
如果每匹馬的實力都不一樣,各自的獲勝機率為\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{64}, \frac{1}{64}, \frac{1}{64}, \frac{1}{64}\),那需要多少資訊量呢?
- 熵
可將之視為對所需訊息量的期望值
- 1~8 號獲勝的概率分別為\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{64}, \frac{1}{64}, \frac{1}{64}, \frac{1}{64}\)
- 猜測 1~8 號馬匹獲勝至少要猜測的次數分別為 1、2、3、4、6、6、6、6
- \(\frac{1}{2}\times1 + \frac{1}{4}\times2 + \frac{1}{8}\times3 + \frac{1}{16}\times4 + \frac{1}{64}\times6 + \frac{1}{64}\times6 + \frac{1}{64}\times6 + \frac{1}{64}\times6 = 2\)
- 也就是猜測出獲勝的馬匹,平均需要 2 次。
4.2.3.2. 熵的計算公式
熵: 資訊量的期望值 \(H(X)=-\sum_{i=1}^{n}P(x_i)\times\log_2 P(x_i) \) 參考上例,以 X 為賽馬編號,則 x 為
\begin{align*} H(X) &= -\frac{1}{2}\times\log_2{\frac{1}{2}} -\frac{1}{4}\times\log_2{\frac{1}{4}} \\ &--\frac{1}{8}\times\log_2{\frac{1}{8}} -\frac{1}{16}\times\log_2{\frac{1}{16}} \\ &-\frac{1}{64}\times\log_2{\frac{1}{64}} -\frac{1}{64}\times\log_2{\frac{1}{64}}\\ &-\frac{1}{64}\times\log_2{\frac{1}{64}}-\frac{1}{64}\times\log_2{\frac{1}{64}}\\ &=2 \end{align*}也就是說: \( Info(D) = -\sum\limits_{i=1}^{m}p_i\times\log_2 p_i \),其中
- D 代表某一個資料集,而這個特徵值會有 1 到 m 種類別,p就是某個類別在這個特徵值中出現的機率。
- 另外在取對數時一般會以 2 為底,源自於資訊的編碼大多是以 0/1 二進位的方式編碼。
- \(p_i\times\log_2 p_i\)的數學意義:某資料出現的機率越低,在 log 的加成下該數值會提高,該數值可以代表人們看到這個資料的驚訝(surprise)程度。
- 例如 1 組數據平常數值都是 1 或 2,但是某一天卻異常出現 99 時,我們就會感到驚訝。
- 當越多令人驚訝的情況出現,整體的不確定性/混亂程度就會提高。
4.2.3.3. 文字的亂度
底下這兩個句子:
the quick brown fox jumps over the lazy dog
與
don’t trouble trouble till trouble troubles you
哪一個的熵值更高?
其資訊熵的計算方式就是:將每個字母的概率與其概率之自然對數相乘,再將每個字母的結果相加,相加之和的負數。可以 python 計算如下7:
1: import math 2: import string 3: import sys 4: 5: def shannon_entropy(data): 6: """ 7: Adapted from http://blog.dkbza.org/2007/05/scanning-data-for-entropy-anomalies.html 8: by way of truffleHog (https://github.com/dxa4481/truffleHog) 9: """ 10: if not data: 11: return 0 12: entropy = 0 13: for x in string.printable: 14: p_x = float(data.count(x)) / len(data) 15: if p_x > 0: 16: entropy += - p_x * math.log(p_x, 2) 17: return entropy 18: 19: sentence1 = 'the quick brown fox jumps over the lazy dog' 20: sentence2 = "don't trouble trouble till trouble troubles you" 21: print(shannon_entropy(sentence1)) 22: print(shannon_entropy(sentence2))
4.385453417442482 3.47695607525754
4.3. 動手計算
讓我們再回到「誰會買筆電」的例子,以 Entropy 來決定還沒完成的第一步:決定要先用哪一項特徵值。這就需要逐一來計算了,其中要用到這個表的資訊,用它來計算幾個熵值。
| 編號 | 年紀 | 收入 | 學生與否 | 購買筆電與否 |
|---|---|---|---|---|
| 1 | <=30 | 高 | 否 | 否 |
| 2 | 31…40 | 高 | 否 | 是 |
| 3 | >40 | 中 | 否 | 是 |
| 4 | >40 | 低 | 是 | 否 |
| 5 | 31…40 | 低 | 是 | 是 |
| 6 | <=30 | 中 | 否 | 否 |
| 7 | <=30 | 低 | 是 | 是 |
| 8 | <=30 | 中 | 是 | 是 |
| 9 | 31…40 | 中 | 否 | 是 |
| 10 | 31…40 | 高 | 是 | 是 |
| 11 | >40 | 中 | 是 | 否 |
4.3.1. 決定第一層
4.3.1.1. 計算購買筆電與否的熵值
| 購買筆電與否 | 出現次數 | \(p_i\) |
|---|---|---|
| 是 | 7 | \(\frac{7}{11}\) |
| 否 | 4 | \(\frac{4}{11}\) |
根據\( Info(D) = -\sum\limits_{i=1}^{m}p_i\times\log_2 p_i \),是否購買(Buy)的熵值為:
\begin{align*} Info(Buy) &= I(7,4) \\ &= -\frac{7}{11}\log_2\frac{7}{11}-\frac{4}{11}\log_2\frac{4}{11} \\ &= 0.425+0.531 \\ &=0.956 \end{align*}4.3.1.2. 計算不同特徵值的熵值
現在我們可以來比較選擇不同特徵值當成樹根的優劣了,我們有以下三種特徵值可以來判斷「購買筆電與否」這個結果:
- 年紀 v.s. 購買筆電與否
- 收入 v.s. 購買筆電與否
- 學生與否 v.s. 購買筆電與否
- 年紀
年紀 購買筆電 未購買筆電 人數 <=30 2 2 4 30~40 4 0 4 >40 1 2 3 不同年紀特徵值(Age)是否購買(Buy)的熵值為:
\begin{align*} Info_{Age}(Buy) &= \frac{4}{11}I(2,2) + \frac{4}{11}I(4,0) + \frac{3}{11}I(1,2) \\ &= \frac{4}{11}(-\frac{2}{4}\log_2\frac{2}{4}-\frac{2}{4}\log_2\frac{2}{4} \\ &+ \frac{4}{11}(-\frac{4}{4}\log_2\frac{4}{4}-\frac{0}{4}\log_2\frac{0}{4} \\ &+ \frac{3}{11}(-\frac{1}{3}\log_2\frac{1}{3}-\frac{2}{3}\log_2\frac{2}{3} \\ &= 0.364 + 0 + 0.250 = 0.614 \end{align*} - 收入
收入 購買筆電 未購買筆電 人數 高 2 1 3 中 3 2 5 低 2 1 3 不同收入特徵值(Income)是否購買(Buy)的熵值為:
\begin{align*} Info_{Income}(Buy) &= \frac{3}{11}I(2,1) + \frac{5}{11}I(3,2) + \frac{3}{11}I(2,1) \\ &= \frac{3}{11}(-\frac{2}{3}\log_2\frac{2}{3}-\frac{1}{3}\log_2\frac{1}{3} \\ &+ \frac{5}{11}(-\frac{3}{5}\log_2\frac{3}{5}-\frac{2}{5}\log_2\frac{2}{5} \\ &+ \frac{3}{11}(-\frac{2}{3}\log_2\frac{2}{3}-\frac{1}{3}\log_2\frac{1}{3} \\ &= 0.250 + 0.441 + 0.250 = 0.941 \end{align*} - 學生與否
學生 購買筆電 未購買筆電 人數 是 4 1 5 否 3 3 6 不同學生特徵值(Student)是否購買(Buy)的熵值為:
\begin{align*} Info_{Student}(Buy) &= \frac{5}{11}I(4,1) + \frac{6}{11}I(3,3) \\ &= \frac{5}{11}(-\frac{4}{5}\log_2\frac{4}{5}-\frac{1}{5}\log_2\frac{1}{5} \\ &+ \frac{6}{11}(-\frac{3}{6}\log_2\frac{3}{6}-\frac{3}{6}\log_2\frac{3}{6} \\ &= 0.498 + 0.545 = 0.953 \end{align*}
4.3.1.3. 以資訊獲利評估合適的第一層特徵值
計算結果:
- 年紀 v.s. 購買筆電與否, 熵=0.614
- 收入 v.s. 購買筆電與否, 熵=0.941
- 學生與否 v.s. 購買筆電與否, 熵=0.953
資訊獲利(information gain)就是用來衡量特徵值於分類資料的能力。依此範例,各項特徵值的資訊獲利計算方式為: 「購買筆電與否的熵」-「某個特徵值下購買筆電與否的熵」。
- 特徵值「年紀」的資訊獲利: 0.956-0.614=0.342
- 特徵值「收入」的資訊獲利: 0.956-0.941=0.015
- 特徵值「學生與否」的資訊獲利: 0.956-0.953=0.003
根據不同特徵值得到的資訊獲利越高,表示該特徵值內資料的凌亂程度越小,用來分類資料效果越佳;反之,若資訊獲利越低,表示該特徵值內資料的凌亂程度越大,用來分類資料效果較差。也就是說:我們應該選年紀來做為第一個決策樹分類值,結果如下圖。
4.3.1.4. 第一次計算成果
在以年紀為第一個決策特徵值的前提下,我們來看看不同年紀下的購買狀況:
| 年紀 | 收入 | 學生與否 | 購買筆電與否 |
|---|---|---|---|
| <=30 | 高 | 否 | 否 |
| <=30 | 中 | 否 | 否 |
| <=30 | 低 | 是 | 是 |
| <=30 | 中 | 是 | 是 |
| 31…40 | 高 | 否 | 是 |
| 31…40 | 低 | 是 | 是 |
| 31…40 | 中 | 否 | 是 |
| 31…40 | 高 | 是 | 是 |
| >40 | 中 | 否 | 是 |
| >40 | 低 | 是 | 否 |
| >40 | 中 | 是 | 否 |
4.3.2. 決定第二層
決定好以年紀做為第一層決策樹特徵值後,接下來就只要考慮
- 收入
- 學生與否
我們來看看針對年紀的三種條件各要以哪一個特徵當成接下來的決策樹特徵?
4.3.2.1. 年紀<=30
先考慮年紀<=30 的狀況
| 年紀 | 收入 | 學生與否 | 購買筆電與否 |
|---|---|---|---|
| <=30 | 高 | 否 | 否 |
| <=30 | 中 | 否 | 否 |
| <=30 | 低 | 是 | 是 |
| <=30 | 中 | 是 | 是 |
- 計算年紀<=30 購買筆電與否的熵值
購買筆電與否 出現次數 出現機率 是 2 \(\frac{2}{4}\) 否 2 \(\frac{2}{4}\) 根據\( Info(D) = -\sum\limits_{i=1}^{m}p_i\times\log_2 p_i \),是否購買(Buy)的熵值為:
\begin{align*} Info(Buy) &= I(2,2) \\ &= -\frac{2}{4}\log_2\frac{2}{4}-\frac{2}{4}\log_2\frac{2}{4} \\ &= 0.5+0.5 \\ &=1 \end{align*} - 計算不同特徵值的熵值
目前有以下兩種特徵值可以來判斷「購買筆電與否」這個結果:
- 收入 v.s. 購買筆電與否
- 學生與否 v.s. 購買筆電與否
- 收入
收入 購買筆電 未購買筆電 人數 高 0 1 1 中 1 1 2 低 1 0 1 不同收入特徵值(Income)是否購買(Buy)的熵值為:
\begin{align*} Info_{Income}(Buy) &= \frac{1}{4}I(0,1) + \frac{2}{4}I(1,1) + \frac{1}{4}I(1,0) \\ &= \frac{1}{4}(-\frac{0}{1}\log_2\frac{0}{1}-\frac{1}{1}\log_2\frac{1}{1} \\ &+ \frac{2}{4}(-\frac{1}{2}\log_2\frac{1}{2}-\frac{1}{2}\log_2\frac{1}{2} \\ &+ \frac{1}{4}(-\frac{1}{1}\log_2\frac{1}{1}-\frac{0}{1}\log_2\frac{0}{1} \\ &= 0 + 0.5 + 0 = 0.5 \end{align*} - 學生與否
學生 購買筆電 未購買筆電 人數 是 2 0 2 否 0 2 2 不同學生特徵值(Student)是否購買(Buy)的熵值為:
\begin{align*} Info_{Student}(Buy) &= \frac{2}{4}I(2,0) + \frac{2}{4}I(0,2) \\ &= \frac{2}{4}(-\frac{2}{2}\log_2\frac{2}{2}-\frac{0}{2}\log_2\frac{0}{2} \\ &+ \frac{2}{4}(-\frac{0}{2}\log_2\frac{0}{2}-\frac{2}{2}\log_2\frac{2}{2} \\ &= 0 + 0 = 0 \end{align*}
- 以資訊獲利評估合適的第二層特徵值
計算結果:
- 收入 v.s. 購買筆電與否, 熵=0.5
- 學生與否 v.s. 購買筆電與否, 熵=0
資訊獲利
- 特徵值「收入」的資訊獲利: 1-0.5 = 0.5
- 特徵值「學生身份」的資訊獲利: 1-0 = 1
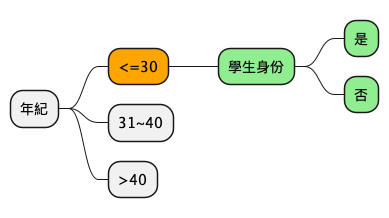
- 需要再分下去嗎?
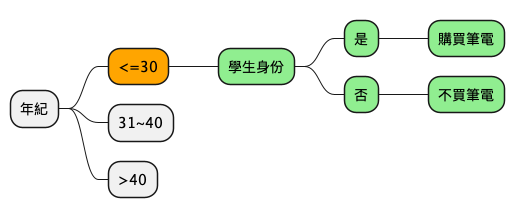
在鎖定了年紀小於 30、學生身份這兩個特徵值後,我們會發現剩下的狀況為:
年紀 學生與否 購買筆電與否 收入 <=30 否 否 高 <=30 否 否 中 <=30 是 是 低 <=30 是 是 中 也就是說,此時的收入已無考慮價值,因為我們已能確定該名顧客是否會購買筆電,即如下圖:
4.3.2.2. 31<=年紀<40
| 年紀 | 收入 | 購買筆電與否 | 學生與否 |
|---|---|---|---|
| 31…40 | 高 | 是 | 否 |
| 31…40 | 低 | 是 | 是 |
| 31…40 | 中 | 是 | 否 |
| 31…40 | 高 | 是 | 是 |
在你急著依照上例手動計算之前,不妨先用力看清楚上面的表,你就會發現其實所有介於這個年齡層的顧客都會購買筆電,所以這就不用再算了…我們會得到底下的部份決策樹:
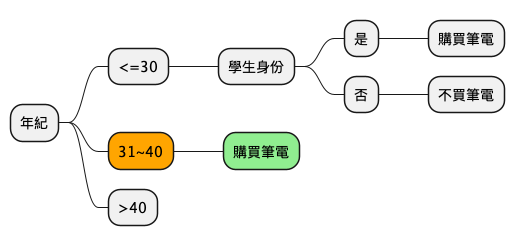
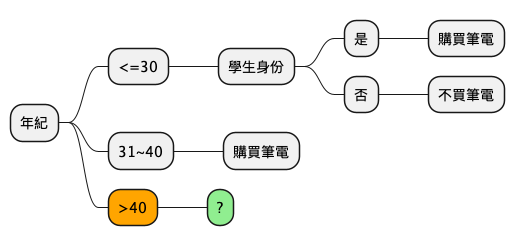
4.3.2.3. [課堂任務]年紀>40 TNFSH
| 年紀 | 收入 | 學生與否 | 購買筆電與否 |
|---|---|---|---|
| >40 | 中 | 否 | 是 |
| >40 | 低 | 是 | 否 |
| >40 | 中 | 是 | 否 |
你不會還在等我把剩下的做完吧?請你和你的組員一起把這棵決策樹完成吧。你可以用 Python、用 Excel、用 Numbers、用計算機、用手算、用心算,請你們利用下課 10 分鐘完作這個作業,並將學習單交到講台。
4.4. Overfitting 問題
- 決策樹很容易產生 Overfitting,如果不限制它,它可以一直長下去分得過細。所以有以下常用的幾種方法來設限
- Minimum samples for a node split:資料數目不得小於多少才能再產生新節點。
- Minimum samples for a terminal node (leaf):要成為葉節點,最少需要多少資料。
- Maximum depth of tree (vertical depth):限制樹的高度最多幾層。
- Maximum number of terminal nodes:限制最終葉節點的數目
- Maximum features to consider for split:在分離節點時,最多考慮幾種特徵值。
4.5. [實作]鳶尾花分類 sklearn
from sklearn.datasets import load_iris from sklearn import tree from sklearn.model_selection import train_test_split # Load in our dataset # # 讀入鳶尾花資料 iris = load_iris() iris_x = iris.data iris_y = iris.target # 切分訓練與測試資料 train_x, test_x, train_y, test_y = train_test_split(iris_x, iris_y, test_size = 0.3) # 建立分類器 # Initialize our decision tree object classification_tree = tree.DecisionTreeClassifier(criterion = "entropy") # Train our decision tree (tree induction + pruning) classification_tree = classification_tree.fit(train_x, train_y) # 預測 test_y_predicted = classification_tree.predict(test_x) print(test_y_predicted) # 標準答案 print(test_y) print('得分:',classification_tree.score(test_x, test_y)) import graphviz import pydot import matplotlib.pyplot as plt #plt.clf() dot_data = tree.export_graphviz(classification_tree, out_file=None, feature_names=iris.feature_names, class_names=iris.target_names, filled=True, rounded=True, special_characters=True) graph = graphviz.Source(dot_data) graph # 這行只適合for colab環境 #graph.render("images/DecisionTree.png", view=True) #graph.format = 'png' #graph.render('images/DecisionTree') #plt.savefig('images/DecisionTree.png', dpi=300)
[0 0 0 0 1 2 0 1 0 2 2 0 2 2 2 2 2 1 1 1 0 2 1 1 2 1 2 2 0 2 0 1 0 2 0 2 2 0 1 1 1 2 2 0 0] [0 0 0 0 1 2 0 1 0 2 2 0 2 2 2 2 2 1 1 1 0 2 1 1 2 1 2 2 0 2 0 1 0 2 0 2 2 0 1 1 1 2 2 0 0] 得分: 1.0
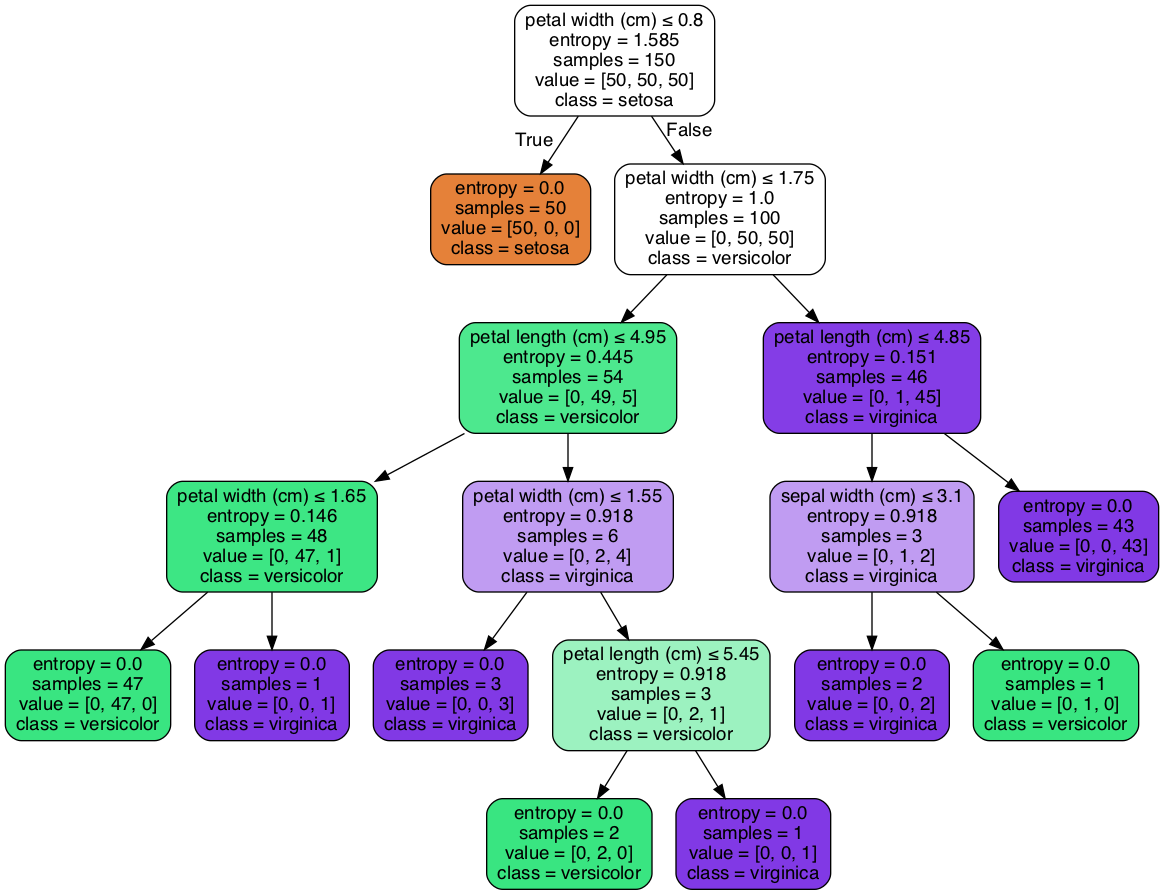
Figure 20: Decision Tree
4.5.1. 關於 classification_tree.score()
- classification_tree.score(test_x, test_y) 是用來計算模型在測試數據上的準確率,表示模型預測正確的比例,取值範圍在 0 到 1 之間。
- 一般來說,0.7(70%) 以上的準確率就算是不錯,但具體標準取決於任務難度和數據集特性。
- 如果數據集不平衡(例如,某個類別佔了大多數),即使高於 0.7 也可能不一定是好結果,這時需要結合其他指標如精確率(Precision)或召回率(Recall)來評估模型。
4.6. [作業]以決策樹進行貸款核淮分析 TNFSH
參考上述程式碼,完成以下任務
- 以 Pandas 讀取貸款訓練資料線上(URL: https://letranger.github.io/AI/images/loantree.csv)
- 移除有缺失值的記錄
- 將 YES/NO、Male/Female 等分類值改為 0/1 值
- 依 Gd,Md,Dd,Ed,SE 這五個特徵值來決定是否核淮貸款申請
- 最終是否核淮貸款的欄位為 LS
- 分別以 Gini index, Entropy 兩種策略來進行分類,比較效能
- 觀察其他特徵值,你有其他的想法可以提高效能嗎?
5. 課堂練習 TNFSH
5.1. 練習一:KNN vs 決策樹分類比較
使用 sklearn 的 Wine(紅酒)資料集,分別以 KNN 和決策樹進行分類,比較兩種演算法的準確率。
Wine 資料集包含 178 筆義大利紅酒的化學成分分析資料,共 13 項特徵(如酒精濃度、蘋果酸含量等),分為 3 個品種。
1: from sklearn.datasets import load_wine 2: from sklearn.model_selection import train_test_split 3: from sklearn.preprocessing import StandardScaler 4: from sklearn.neighbors import KNeighborsClassifier 5: from sklearn.tree import DecisionTreeClassifier 6: 7: # 載入資料 8: wine = load_wine() 9: X, y = wine.data, wine.target 10: 11: # 切分資料(80% 訓練、20% 測試) 12: X_train, X_test, y_train, y_test = train_test_split( 13: X, y, test_size=0.2, random_state=42) 14: 15: # 標準化(KNN 對尺度敏感,決策樹不受影響) 16: scaler = StandardScaler() 17: X_train_scaled = scaler.fit_transform(X_train) 18: X_test_scaled = scaler.transform(X_test) 19: 20: # --- 請在此完成 KNN 分類器(k=5)--- 21: 22: 23: # --- 請在此完成決策樹分類器(max_depth=3)--- 24: 25: 26: # 比較結果,想一想: 27: # 1. 哪一種分類器的準確率較高? 28: # 2. 如果不做標準化,KNN 的結果會怎樣?決策樹呢?
5.2. 練習二:用 Python 計算 Information Gain
下面有一組簡單的資料:10 位學生的「是否住校」「是否有社團」與「期末是否及格」的記錄。請用 Python 計算各特徵的 Information Gain,決定哪個特徵最適合作為決策樹的第一個分割條件。
| 編號 | 住校 | 社團 | 及格 |
|---|---|---|---|
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 是 |
| 4 | 是 | 否 | 否 |
| 5 | 否 | 是 | 是 |
| 6 | 否 | 是 | 否 |
| 7 | 否 | 否 | 否 |
| 8 | 否 | 否 | 否 |
| 9 | 否 | 否 | 否 |
| 10 | 是 | 否 | 是 |
提示:
- 熵公式:\( H(X) = -\sum p_i \log_2 p_i \)
- Information Gain = 整體的熵 − 以某特徵分割後的加權熵
1: import math 2: 3: def entropy(positive, negative): 4: """計算熵值""" 5: total = positive + negative 6: if total == 0: 7: return 0 8: p_pos = positive / total 9: p_neg = negative / total 10: e = 0 11: if p_pos > 0: 12: e -= p_pos * math.log2(p_pos) 13: if p_neg > 0: 14: e -= p_neg * math.log2(p_neg) 15: return e 16: 17: # 整體資料:及格 5 人、不及格 5 人 18: total_entropy = entropy(5, 5) 19: print(f'整體熵值: {total_entropy:.4f}') 20: 21: # --- 請計算「住校」的 Information Gain --- 22: # 住校=是(共 5 人):及格 ? 人、不及格 ? 人 23: # 住校=否(共 5 人):及格 ? 人、不及格 ? 人 24: 25: 26: # --- 請計算「社團」的 Information Gain --- 27: # 社團=是(共 4 人):及格 ? 人、不及格 ? 人 28: # 社團=否(共 6 人):及格 ? 人、不及格 ? 人 29: 30: 31: # 哪個特徵的 Information Gain 較高?應該選哪個當樹根?
6. [卜聖卦活動3]以分類預測學校 TNFSH
6.1. 資料集介紹
這份資料集記錄了某校近三年三年級學生的國文、英文、數學成績,以及他們實際錄取的學校:
- 國文、英文、數學為數值型資料
- 錄取學校為分類標籤(Label)
- 檔案下載連結:3yScTest2.csv
6.2. 任務說明
請依照下列步驟完成分類任務,預測學生將錄取哪所學校:
- 觀察資料結構
- 刪除缺失值(例如錄取學校為 “-”)
- 過濾樣本太少的類別
- 把「錄取人數少於 20 人」的學校刪除
- 這樣可以避免模型因資料太少而無法有效學習
- 切分資料集 以 8:2 的比例分割訓練集與測試集
6.3. 作業提交說明
完成分類後,請計算你們模型的分類準確率(Accuracy)並回報下列格式:
1: # 進行預測 2: y_pred = model.predict(X_test) 3: 4: # 評估準確率 5: from sklearn.metrics import accuracy_score 6: accuracy = accuracy_score(y_test, y_pred) 7: 8: # 作業回報 9: # 本組最高 Accuracy 為: 0.8732
6.4. 開始吧!
1: import pandas as pd 2: import numpy as np 3: 4: # 載入資料 5: df = pd.read_csv('https://letranger.github.io/AI/Downloads/3yScTest2.csv') 6: df.head()
Footnotes:
Hands-On Machine Learning with Scikit-Learn: Aurelien Geron