迴歸
Table of Contents
1. 關於迴歸
當我們談到「迴歸」時,意思是根據一組預測特徵(feature),像是里程數、車齡、品牌等等,來預測一個連續的數值目標,例如二手車的售價。也可以是像根據歷史股價來預測明天的股價,或者根據即時路況來預測車子的轉向角度和速度。
有些迴歸演算法其實也可以拿來做分類的工作。像是 Logistic Regression,它會輸出一個介於 0 到 1 之間的數值,這個數值可以解釋成「某件事情發生的機率」。舉例來說,我們可以用它來判斷一封 email 是不是垃圾郵件,比如說判斷結果是 0.2,那就代表這封信有 20% 的機率是垃圾信;又或者是判斷一張圖片裡是不是狗,結果是 0.7,那代表有 70% 的機率是狗。
1.1. 迴歸類型
在機器學習裡,迴歸問題指的是:根據一組「預測特徵」(如:車子的里程數、車齡、品牌)來預測一個連續數值(如:二手車車價)。又如:
- 根據歷史股價預測明天股價
- 根據即時路況預測車速或方向盤轉向角度
迴歸問題可分為兩類:
- Linear Regression(線性迴歸)
- Logistic Regression(邏輯斯迴歸)
1.1.1. Linear regression:
- 假設輸入變量(x)與單一輸出變量(y)間存在線性關係,並以此建立模型。
- 優點: 簡單、容易解釋
- 缺點: 當輸入與輸出變量間的關係為非線性時會導致低度擬合
- 例: 預測某人身高與體重的關係
Linear regression可再細分為
Simple Linear regression (簡單線性迴歸):
只討論一個輸入變數與一個輸出變數的關係
Multiple Linear regression (多元線性迴歸)
當有多個輸入變數 \(x_1, x_2, ..., x_n\) 一起影響輸出 \(y\) 時,就用多元線性迴歸來建模:
\[y=ax_1+bx_2+cx_3+⋯+zx_n+\epsilon\]
其中:
- \(y\) :輸出變量(應變數)
- \(x_1, x_2, \dots\) :輸入變量(特徵值)
- \(a, b, c, \dots\) :權重(係數)
- \(\epsilon\) :誤差項(residual)
多元迴歸是線性迴歸的一種延伸,其模型結構如圖1所示,輸入變量 \(x_1, x_2, x_3\) 分別對應到權重 \(a, b, c\),最終輸出變量 \(y\)。這種模型可以用來預測多個特徵值對應的輸出結果。
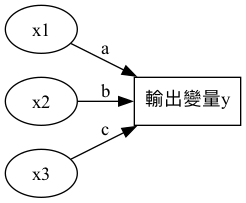
Figure 1: 多元線性迴歸模型
1.1.2. Logistic Regression(邏輯斯迴歸)
是一種線性模型,但最終會通過 sigmoid 函數把預測結果轉為 0~1 的機率值,適合處理二元分類問題
- 優點:簡單、可解釋性高
- 缺點:
資料特徵與分類結果間若為非線性關係,表現會不佳
1.1.3. 迴歸的目的
建立迴歸的目的在於從現有資料中找出規則,然後依此規則來對後續的新進資料進行預測。我們想做的事,是根據過去的資料找出某種規律,接著用這個規律來預測未來的新資料。
圖2中有一些資料分佈,x、y軸為資料的兩個特徵值。這些資料點的分佈並不是隨機的,而是有某種規律可循。這些資料點可能代表了某個現象或事件的特徵,例如房價、股價、氣溫等等。
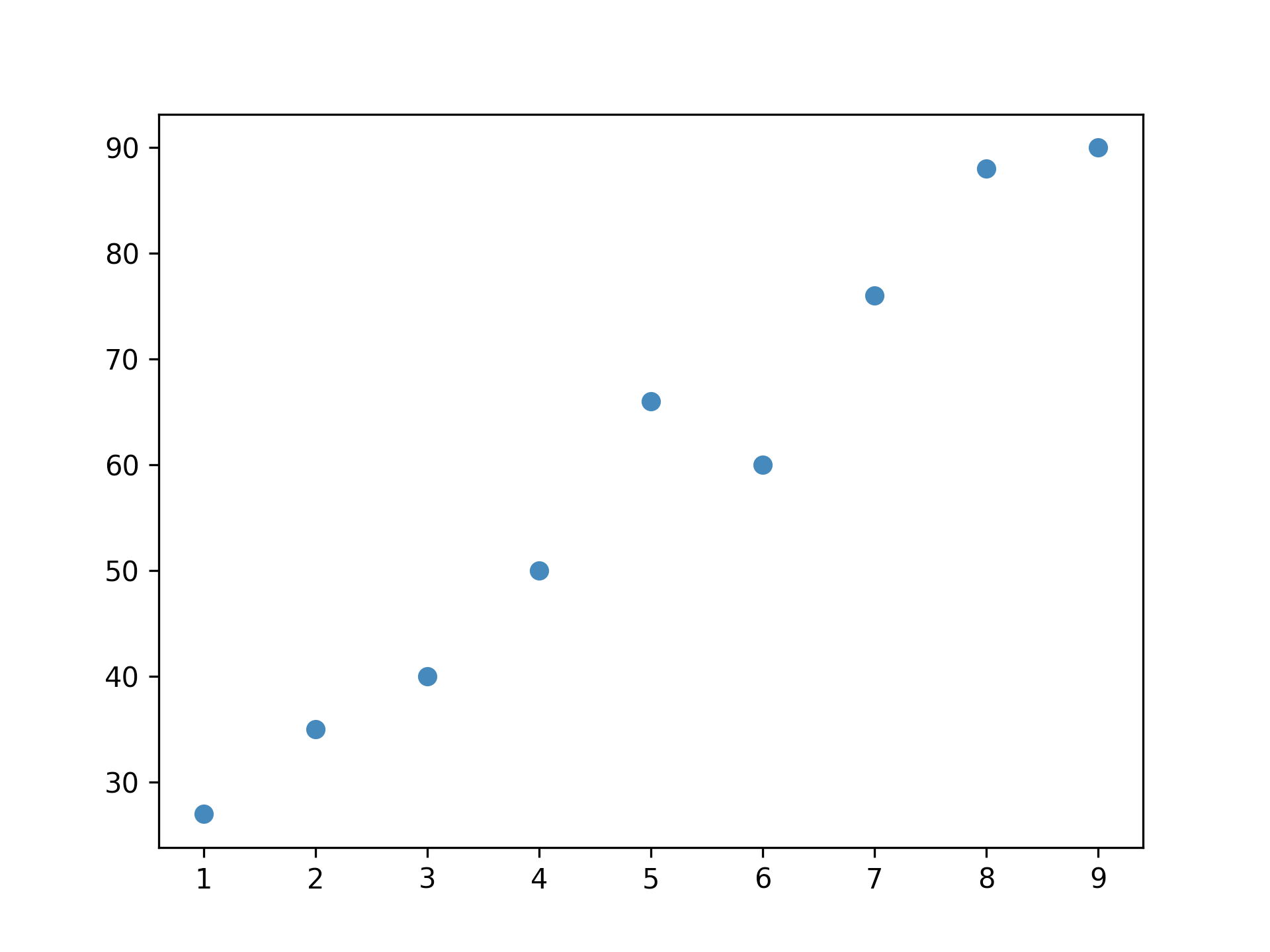
Figure 2: 原始資料分佈
我們可以畫出幾條直線來代表這些資料的趨勢,問題是:
- 怎麼畫
- 怎麼知道哪一條最有代表性
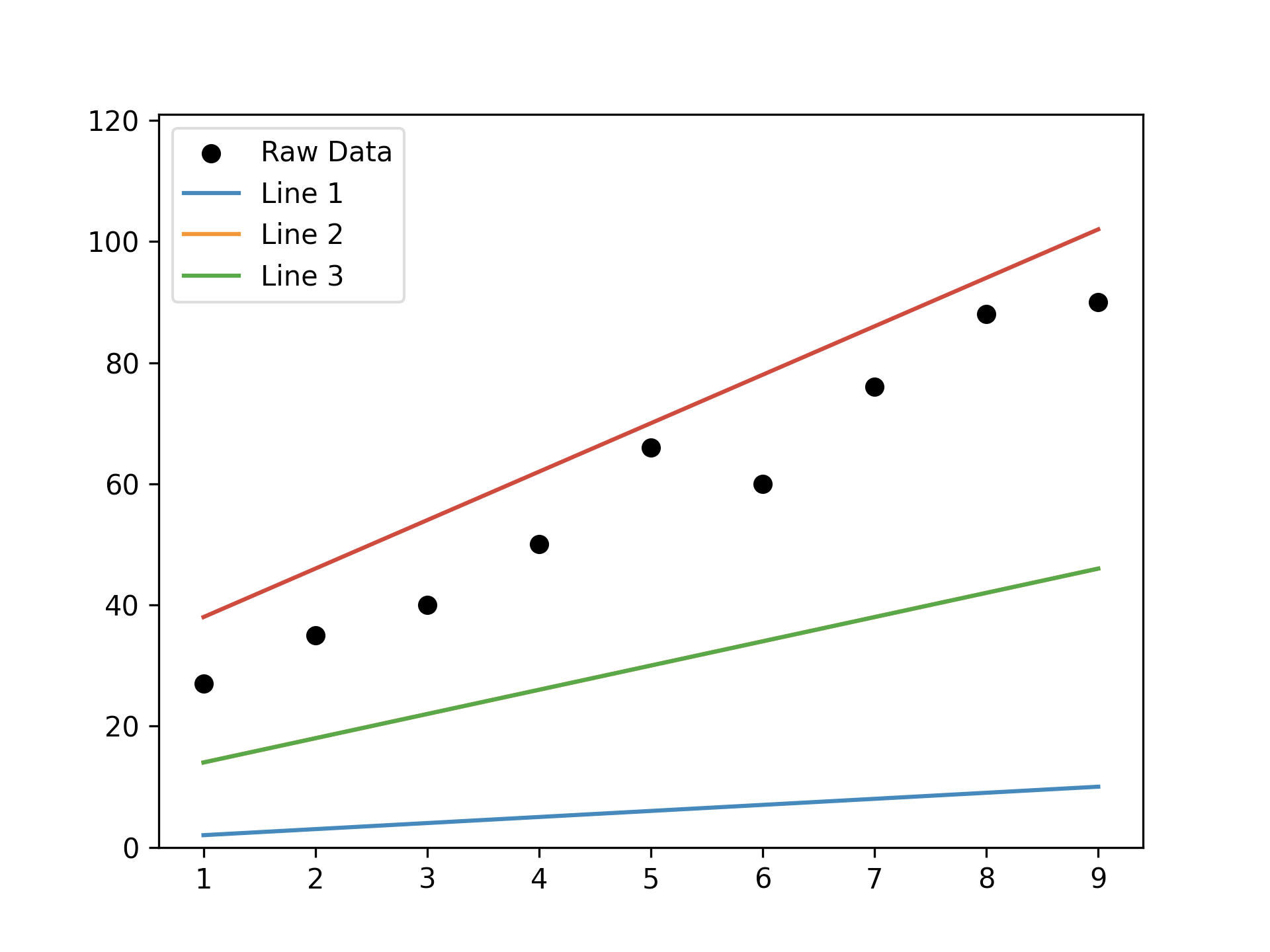
Figure 3: 根據原始資料畫出的幾條迴歸線
迴歸就是想解決這些問題。它的目的是從一組資料中找出一條最能代表這些資料的直線(或曲線),然後用這條線來預測未來的新資料。常見應用案例:
- 波士頓房價預測(Boston Housing Dataset)
- 股票價格預測
- 天氣數據分析
- 車輛油耗預測
2. 迴歸原理
在學習投籃時,我們會不斷修正自己的手感與角度,觀察球飛出後落點和籃框的誤差,然後做出調整。其實機器學習的原理也很像──我們要讓電腦學會預測,步驟如下:
- 建立一個初步的模型(就像第一次隨便丟一球)
- 看它丟得準不準(計算誤差)
- 再根據誤差做調整(優化模型)
2.1. Step 1:模型與資料
2.1.1. 模型 Model:
我們先假設一個最簡單的模型,例如:\[f(x)=y=w⋅x+b\]
這就像是說:「我先用這種方法來丟看看。」
然而,像 \(f(x)=y=w⋅x+b\) 這樣的模型有無限多種可能性,因為我們可以隨意調整參數 \(w\) 和 \(b\)。所以我們需要一個方法來評估這個模型的好壞。這就是我們接下來要做的事。
2.2. Step 2:看這個方法丟得好不好(評估函數)
- 訓練資料 Training Data:
我們把這些 \(x\) 值輸入模型,看看預測的 \(\hat{y}\) 值跟真實的 \(y\) 差多少。 - 損失函數 Loss Function \(L\) :
用來衡量模型預測得有多爛。它的工作就像「計分員」一樣,分數越高表示錯越多,越低代表模型越準。所以我們希望 \(L\) 越小越好。 挑選最好的模型 \(f*\) :
我們的目標是找到一個讓 Loss 最小的模型:
\[f∗=\argminL(f)\]
意思是:「從所有可能的模型中,挑出那個讓損失函數值最小的。」
- 數值解法:梯度下降法 Gradient Descent
如果沒辦法直接算出最小值(因為函數太複雜),我們就用「試著一點一點往低處爬」的方式找答案。
想像我們在一個山谷裡,摸黑想找到最低點(最小誤差),每次往斜坡最陡的方向走一小步,這就是 梯度下降法(Gradient Descent) 的精神。
3. 線性迴歸: 學期成績預估
接下來就以學期成績預估為例,來介紹迴歸的概念與實作。
3.1. 函數: AI的本質
前面提及我們希望找出一個函數\(f(x)\),事實上,人工智慧本質上就是在找出一個特定函數。例如,我們想利用人工智慧來預估自己這個學期的資訊科成績,而根據歷屆學長的口耳相傳,某科教師給定學期總成績的方式似乎與「期中考、期末考平均」有直接的關係。
所以現在的問題就簡化為:找一個類似這樣的函數:
\[f(兩次段考平均成績)→學期總成績\]
有了這個函數,只要我們輸入這學期的兩次段平均成績,就能算出自己的學期總成績。但像這樣的函數f有無限多個,其中一種可能的計算方式如下:
\[期末成績=0.4×兩次段考平均成績\]
,此處的0.4就稱為這個函數的參數(parameter)。
其實,我們的目的就是在找出一個函數 \(f(x)=ax\),其中的 \(x\) 為兩次段考平均成績,\(a\) 為參數,這個函數能夠將兩次段考平均成績轉換為學期總成績。
為了找出這個函數,我們首先應蒐集歷屆學長姐的成績資料(包括兩次段考平均成績與學期總成績),這些資料稱之為訓練資料(training data)。
在將訓練資料視覺化後,我們發現x與y的分佈如圖4所示(假設我們詢問了10位學長姐、收集了10筆訓練資料),初步猜測二者可能存在線性關係。
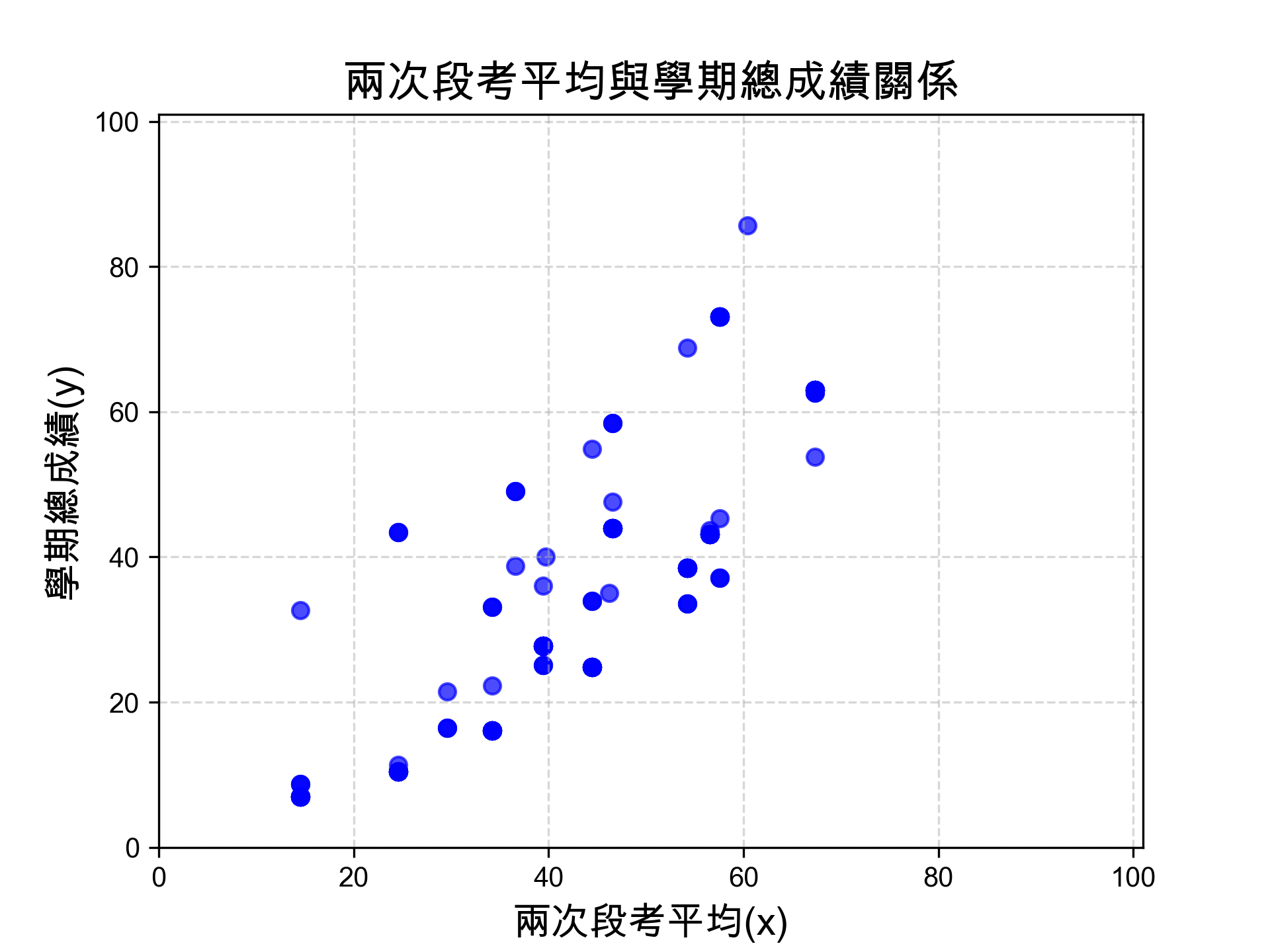
Figure 4: 兩次段考平均與學期總成績關係
接下來的任務就是畫出一條能儘量接近圖上所有資料點的線,也就是找出最佳的參數a(即這條迴歸線的斜率)。
3.2. 逐步找出最佳的a
雖然在此例中最佳的 \(a\) 可以很快用數學公式求出,但此處我們打算介紹另一種逐步找出最佳 \(a\) 的方式,步驟詳列如下:
3.2.1. \(a=0.5\)
首先,面對未知的困難,我們要有嚴格的解題SOP,也就是要遵循「科學、理性、務實」的精神: 閉著眼睛隨便給個 \(a\) 。
假設這次我們瞎矇到的 \(a\) 值為0.5,畫出的迴歸線結果如圖5。
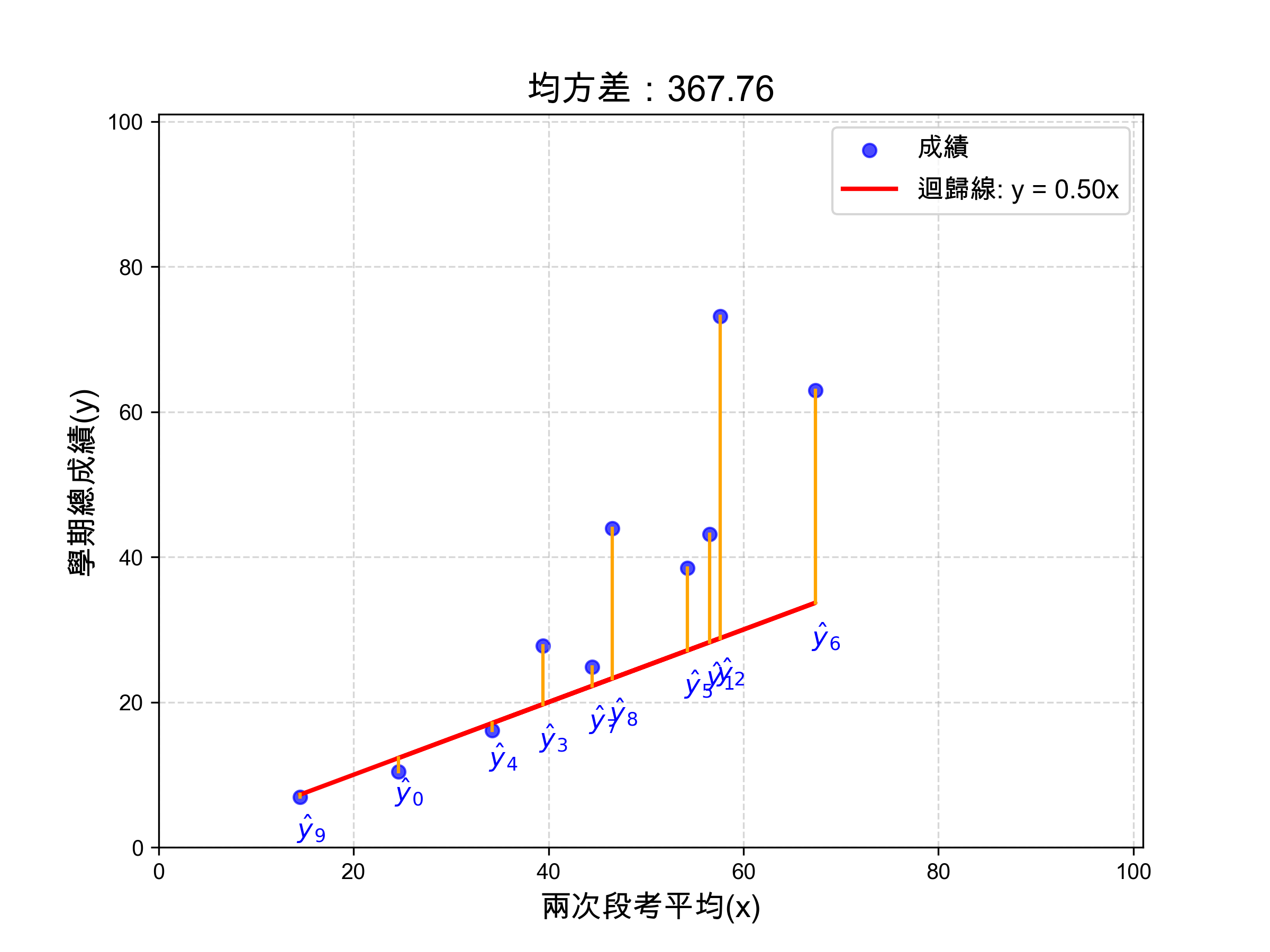
Figure 5: a=0.5的迴歸線
有了這條迴歸線(也就是我們的模型)之後,我們就可以來評估它的好壞了。
做法很簡單:我們把每一筆資料的預測值,和實際值相比,看看點到這條線有多遠。理想情況下,我們當然希望每個點都離這條線越近越好,代表模型預測得很準。
在圖 5 中,橘色的線段就是每一筆資料點到預測線的距離,我們把這些距離加總起來,就是這條線「預測得有多差」的總誤差。此處以均方差(Mean Squared Error, MSE)來計算,誤差值為367.76。MSE公式如下:
\[MSE=\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y_i})}^2\]
,這裡的MSE就是這個模型的損失函數(Loss Function),其中:
- \(y_i\) 是第 \(i\) 筆資料的真實值
- \(\hat{y_i}\) 是模型預測出來的值
- \(n\) 是總資料筆數
這個 MSE 數值就是我們這個模型的損失函數(Loss Function)。數值越小,表示預測越準;數值越大,表示預測越差。
例如:某次模型的 MSE 計算結果為 367.76,這就代表目前這條迴歸線預測得還有不少偏差,我們就需要進一步調整模型參數 \(a\) 。
3.2.2. \(a=0.4, a=0.6\)
但是目前的 \(a=0.5\) 就是我們能找到的最好迴歸線(模型)嗎? 沒有比較就沒有傷害,就像你以為以前選出的立委已經很爛了,最後才發現總是能選出更爛的。
為了找出更好的迴歸線,我們可以試著調整 \(a\) 的值,看看能不能找到更小的誤差。方法也很簡單,我們一樣用「科學、理性、務實」的精神,隨便這個 \(a\) 各加、減0.1,再來觀察誤差的變化。至於為什麼是它各加、減0.1?都跟你說了這是「科學、理性、務實」、這是信仰,而信仰是不容質疑的,你接受就好。
結果如圖6,可以發現a再大一些結果似乎會更好。
各個a值所對應的MSE結果如下:
a = 0.1, MSE = 1297.99 a = 0.2, MSE = 1000.40 a = 0.3, MSE = 746.17 a = 0.4, MSE = 535.29 a = 0.5, MSE = 367.76 a = 0.6, MSE = 243.59 a = 0.7, MSE = 162.78 a = 0.8, MSE = 125.32 a = 0.9, MSE = 131.21 a = 1.0, MSE = 180.46 a = 1.1, MSE = 273.07 a = 1.2, MSE = 409.03 a = 1.3, MSE = 588.35 a = 1.4, MSE = 811.02 最小 MSE 發生在 a = 0.80,MSE = 125.32 圖檔輸出至: images/mse_series.png
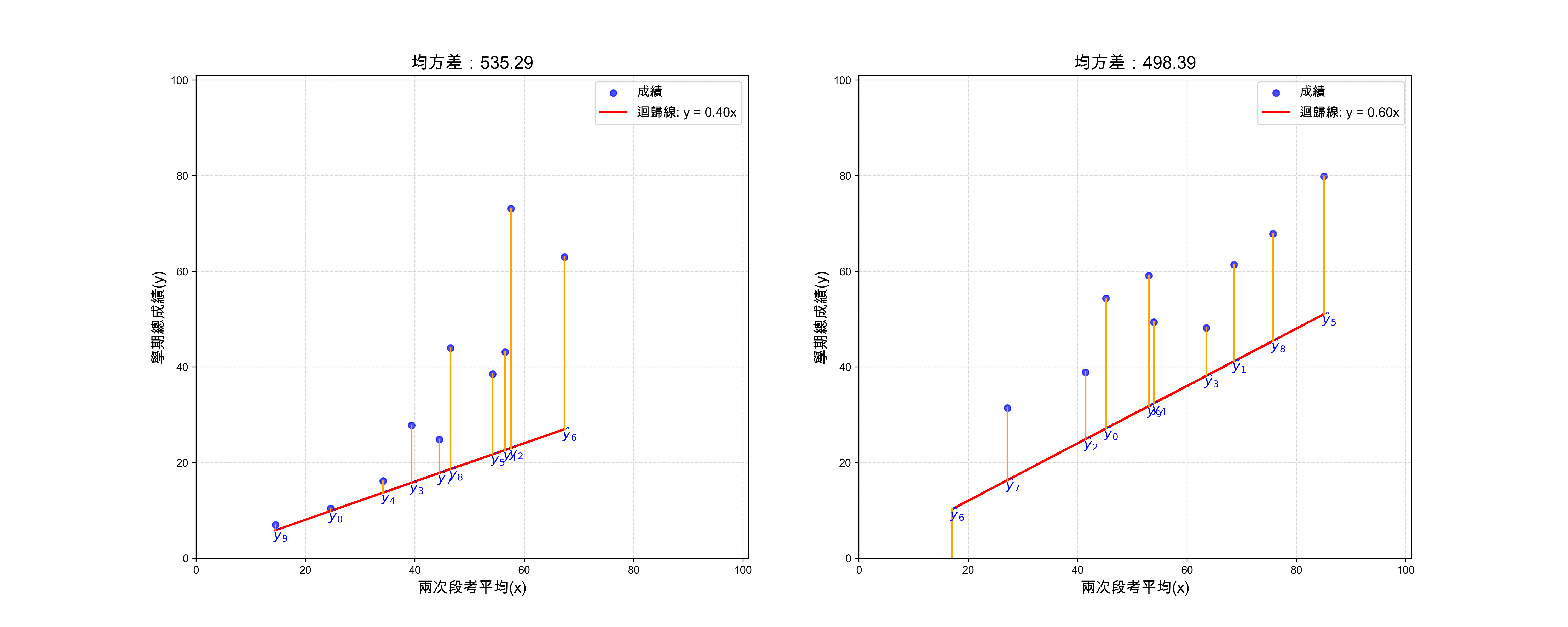
Figure 6: a=0.4 v.s. a=0.6
3.2.3. 評估所有可能的 \(a\)
當我們把全部合理的 \(a\) 值(如\(0.3 \le a \le 1.4\))對應的損失函數逐一計算出來後,就可以將這些結果畫成一條如圖7的曲線,這就是這個模型的損失函數曲線(Loss Function Curve)。
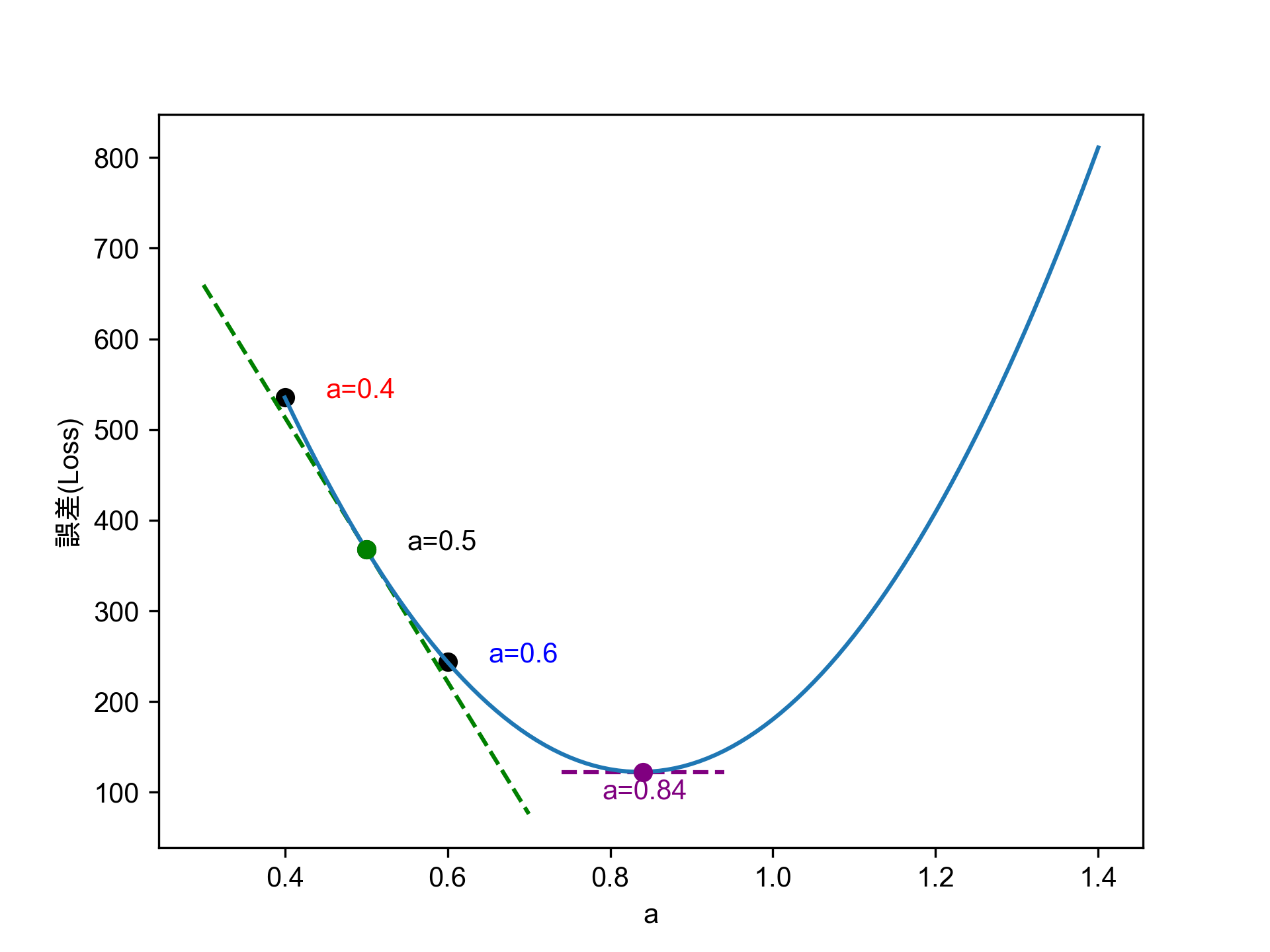
Figure 7: 合理a值畫出的誤差函數
不難看出:只要將 \(a\) 逐步往損失函數較小的方向調整,這個模型的預測效果就會更好。
另一種調整 \(a\) 值的方式是透過資料點在曲線上的切線(圖中綠色虛線)斜率來判斷該往左或右移動 \(a\) 值,直到找到切線斜率為0的點,這便是曲線的最低點,也是最佳 \(a\) 值。此函數如下,也是我們用來預估分數的模型:
\[y=f\left(x\right)=0.84x\]
3.3. 兩個參數的模型
前一個例子有點太簡單了,只有一個參數 \(a\),實際上我們的模型通常會更複雜一些。
假設這位老師忽然良心發現,覺得不應該用這麼草率的計分方式來決定學生是否能取得學分。於是他將學期成績的計分方式改為「分別對期中考、期末考成績進行加權」。此時我們的模型就變成了兩個參數 \(a\) 和 \(b\),函數如下:
\[y=f\left(x\right)=ax_1+bx_2\]
,其中
- \(x_1\) 為期中考成績
- \(x_2\) 為期末考成績
- \(y\) 為學期總成績
而我們的任務在求出最佳的參數 \(a, b\)。
比照上述步驟的做法,我們可以求出所有合理的 \(a, b\) 值(0~1)及其所對應的損失函數,將結果畫成如圖8的曲面。
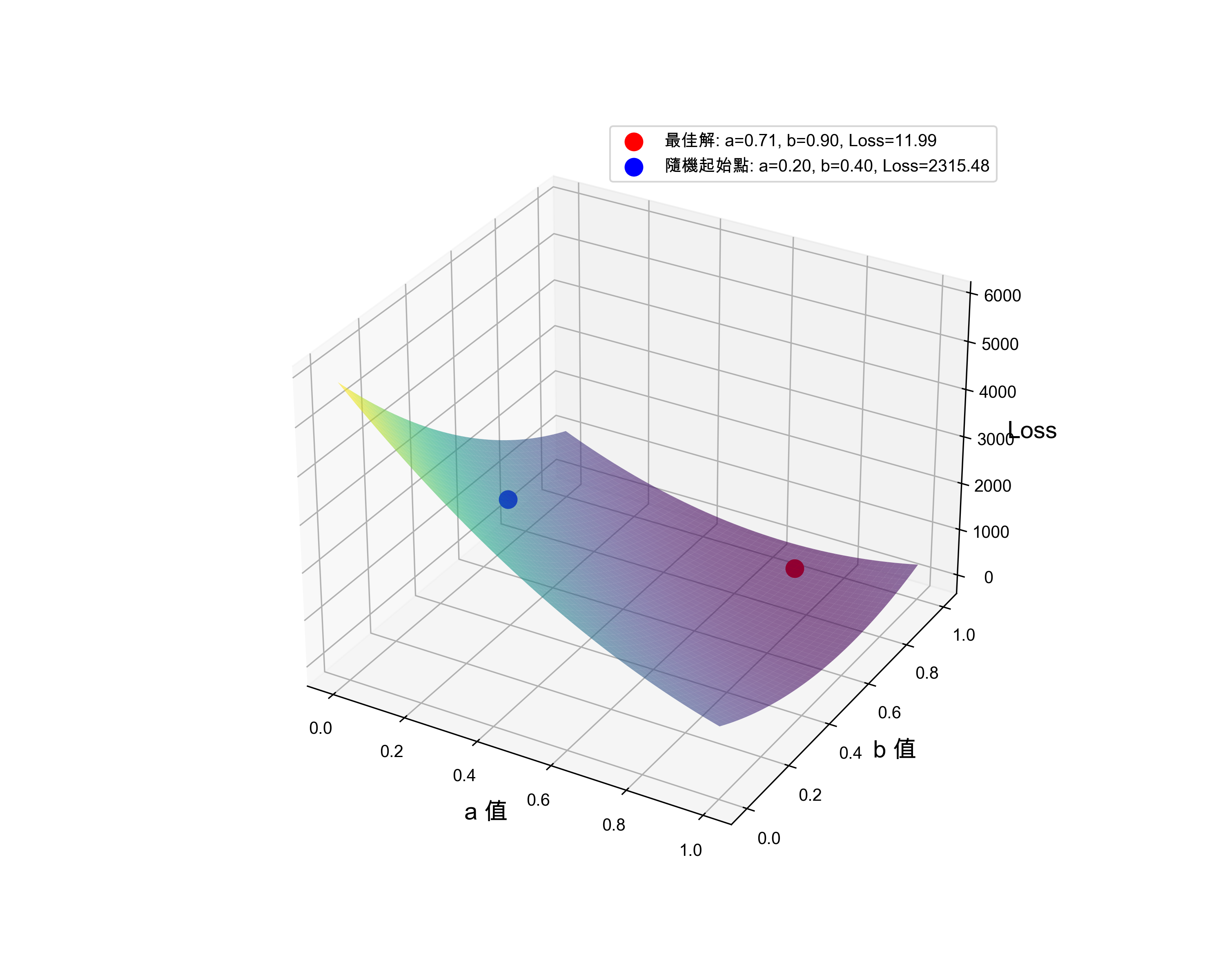
Figure 8: 兩個參數時的誤差函數
實際求解時,一樣先隨機指定一組權重值 \(a, b\)(圖8藍色點),依該點在曲面上的斜率(此處稱為梯度,Gradient) ,沿著梯度的反方向往下找,就能找到這個曲面的最低點(圖8紅色點),該點便是函數的最佳參數。
此種做法也就是神經網路中找出模型最佳參數的核心思想:梯度下降法(Gradient Descent)。
3.4. 神經網路的視角
從神經網路的角度來看,上述函數也可以視為如圖9的模型,模型中只有一層隱藏層,裡面只有一個神經元,輸出結果為期末成績,這便是一個能進行迴歸計算的神經網路。
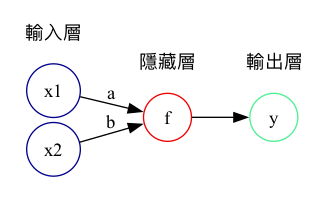
Figure 9: 以兩項成績預估學期成績的神經網路
4. 線性迴歸實作: 波士頓房價預測
- 本例中部份程式碼及文字來自What impacts Boston Housing Prices
- 本例使用資料集為 1970 年中期 Boston 郊區資料,包含犯罪率、當地財產稅等,用以預測某郊區房價中位數,本例有 506 筆資料,分為 404 個訓練樣本和 102 個測試樣本,但每個 feature 的單位不同,故須先進行資料預調整。
4.1. 下載資料
1: import pandas as pd 2: 3: housing = pd.read_csv('https://raw.githubusercontent.com/letranger/AI/gh-pages/Downloads/boston_housing.csv')
也可以用tensorflow的load_data()直接下載,但這組沒有column title
1: import matplotlib.pyplot as plt 2: from tensorflow.keras.datasets import boston_housing 3: 4: (train_x, train_y), (test_x, test_y) = boston_housing.load_data()
4.2. 大概觀察一下資料集
1: print(type(housing)) 2: print(housing.shape) 3: print(housing.iloc[0])
<class 'pandas.core.frame.DataFrame'> (506, 14) crim 0.00632 zn 18.00000 indus 2.31000 chas 0.00000 nox 0.53800 rm 6.57500 age 65.20000 dis 4.09000 rad 1.00000 tax 296.00000 ptratio 15.30000 b 396.90000 lstat 4.98000 medv 24.00000 Name: 0, dtype: float64
這個資料集共有506筆資料,前13個為特徵值,最後一個medv為房價。其他特徵值分別代表:
- CRIM: 每個城鎮的人均犯罪率
- ZN: 佔地超過 25,000 平方英尺的住宅用地比例
- INDUS: 每個城鎮的非零售業商業用地比例(工業區)
- CHAS: 查爾斯河虛擬變量(= 1 如果地段邊界是河流;否則為 0)
- NOX: 一氧化氮濃度(每 1000 萬分之一)
- RM: 每套住宅的平均房間數
- AGE: 1940 年前建成的自有住宅單位比例
- DIS: 到五個波士頓就業中心的加權距離
- RAD: 徑向公路可達性指數
- TAX: 每 $10,000 的全價房產稅率
- PTRATIO: 每個城鎮的師生比例
- B: 1000(Bk - 0.63)^2,其中 Bk 是每個城鎮的黑人比例
- LSTAT: 低社會地位人口的百分比
- MEDV: 房值(以 $1000 為單位)
4.3. 資料預處理
4.3.1. 處理缺漏值
快速檢查是否有缺漏值
1: print(housing.isnull().sum())
crim 0 zn 0 indus 0 chas 0 nox 0 rm 0 age 0 dis 0 rad 0 tax 0 ptratio 0 b 0 lstat 0 medv 54 dtype: int64
刪掉有缺失值的資料
1: housing.dropna(axis=0, inplace=True) 2: print(housing.isnull().sum()) 3: print(housing.shape)
crim 0 zn 0 indus 0 chas 0 nox 0 rm 0 age 0 dis 0 rad 0 tax 0 ptratio 0 b 0 lstat 0 medv 0 dtype: int64 (452, 14)
4.3.2. 資料標準化
由第一筆訓練資料特徵housing.iloc[0]可以看出,每項特徵值的差異甚大,我們可以先對這些資料特徵進行標準化:
1: print(housing.iloc[0,:-1]) 2: 3: mean = housing.iloc[:,:-1].mean(axis=0) 4: housing.iloc[:,:-1] -= mean 5: std = housing.iloc[:,:-1].std(axis=0) 6: housing.iloc[:,:-1] /= std 7: 8: print(housing.iloc[0,:-1])
crim 0.00632
zn 18.00000
indus 2.31000
chas 0.00000
nox 0.53800
rm 6.57500
age 65.20000
dis 4.09000
rad 1.00000
tax 296.00000
ptratio 15.30000
b 396.90000
lstat 4.98000
Name: 0, dtype: float64
<string>:5: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value '0 -6.823009
1 -5.823009
2 -5.823009
3 -4.823009
4 -4.823009
...
501 -6.823009
502 -6.823009
503 -6.823009
504 -6.823009
505 -6.823009
Name: rad, Length: 452, dtype: float64' has dtype incompatible with int64, please explicitly cast to a compatible dtype first.
crim -0.566733
zn 0.217000
indus -1.176220
chas -0.289391
nox -0.024739
rm 0.347120
age -0.012727
dis 0.022210
rad -0.904489
tax -0.538187
ptratio -1.339563
b 0.394920
lstat -1.049614
Name: 0, dtype: float64
4.4. 觀察資料
4.4.1. 初步看一下房價的分佈
1: import matplotlib.pyplot as plt 2: import seaborn as sns 3: 4: sns.histplot(housing['medv']) 5: plt.savefig("images/housing-price.png", dpi=300)
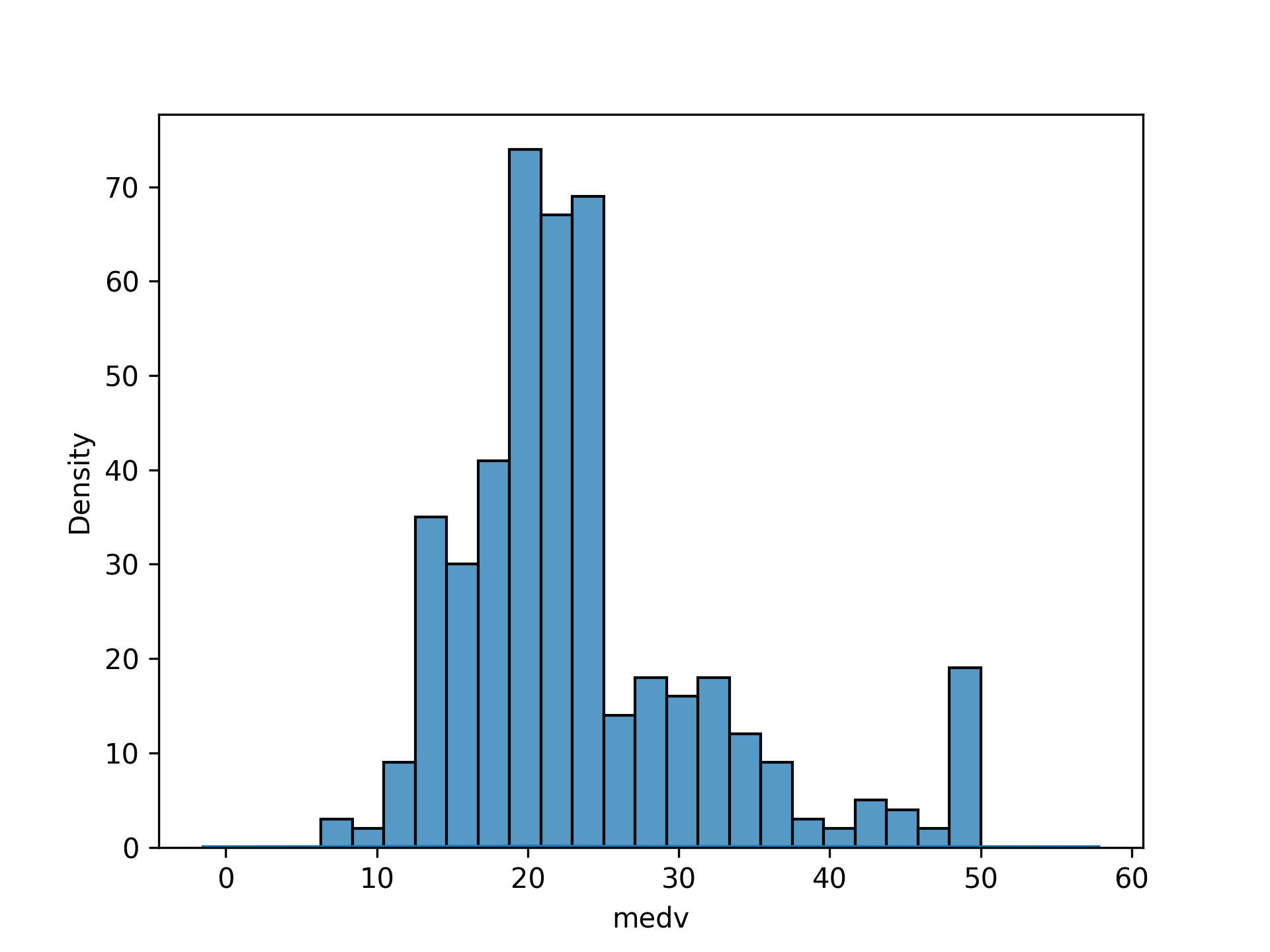
Figure 10: 房價分佈概況
4.4.2. 各特徵值間的關係
1: correlation_matrix = housing.corr().round(2) 2: # annot = True 讓我們可以把數字標進每個格子裡 3: sns.heatmap(data=correlation_matrix, annot = True) 4: plt.savefig("images/housing-corr.png", dpi=300)
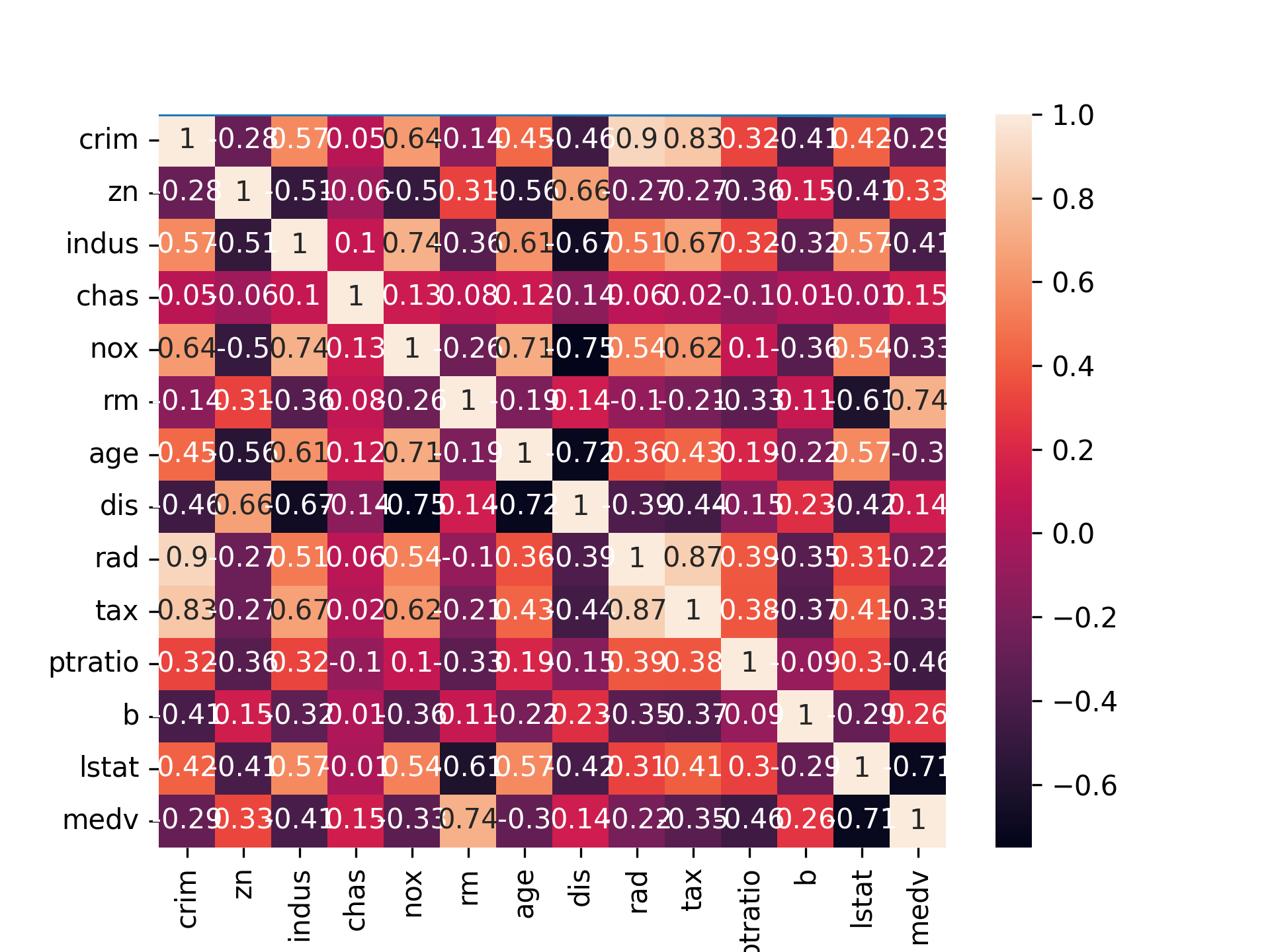
Figure 11: 特徵值間的關係
由圖11可以看出:
- 跟MEDV(房價)高度相關的是LSTAT(中低收入戶佔當地居住人口的比例)和RM(房子有幾間房間)這兩個變數。
- 此外也看到DIS(到波士頓商業中心的距離)和AGE(屋齡),INDUS(非零售業土地使用比例)和ZN(居住使用土地比例)這兩組變數有多元共線性問題,所以未來如果要做其他模型,避免同時使用這兩組中的變數。
所以我們 直覺的想法 是:應該可以用LSTAT和RM來做出預測MEDV的模型。再次把這兩個變數跟房價變數的關係畫出來,可以看到兩者和房價變數都接近線性關係:
1: # 設定整張圖的長寬 2: plt.figure(figsize=(20, 10)) 3: features = ['lstat', 'rm'] 4: target = housing['medv'] 5: for i, col in enumerate(features): 6: # 排版1 row, 2 columns, nth plot:在jupyter notebook上兩張並排 7: plt.subplot(1, len(features) , i+1) 8: # add data column into plot 9: x = housing[col] 10: y = target 11: plt.scatter(x, y, marker='o') 12: plt.title(col) 13: plt.xlabel(col) 14: plt.ylabel('medv') 15: plt.savefig('images/housing-2var.png', dpi=300)
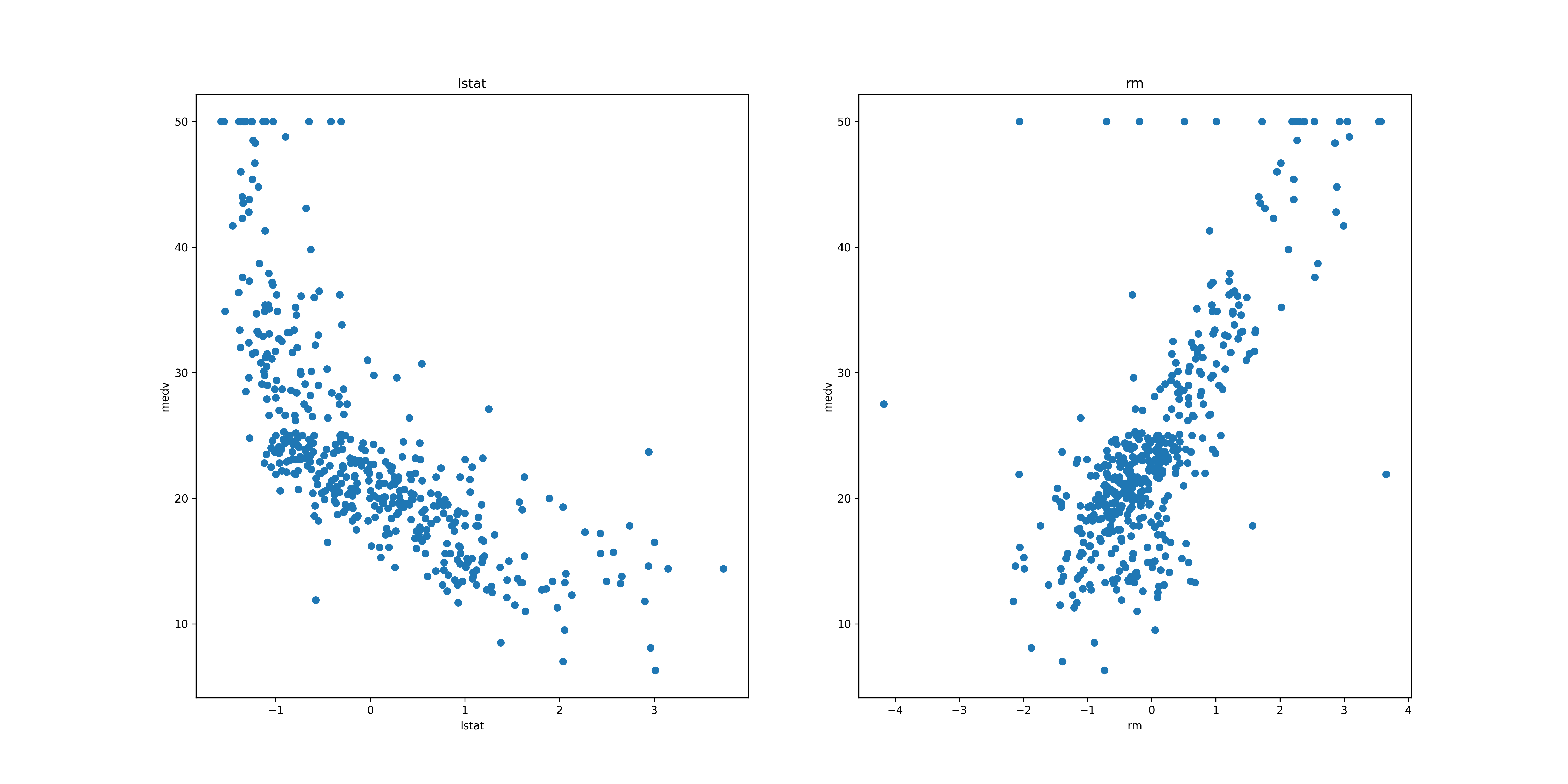
Figure 12: LSTAT和RM與房價的關係
4.4.3. 準備訓練用的資料
先拿兩項特徵值來試一下水溫: lstat和rm
1: import numpy as np 2: X = housing[['lstat', 'rm']] 3: Y = housing['medv'] 4: print(X) 5: print(Y)
lstat rm
0 -1.049614 0.347120
1 -0.373898 0.116169
2 -1.203924 1.261927
3 -1.380974 0.981486
4 -0.992763 1.204939
.. ... ...
501 -0.287809 0.374115
502 -0.383644 -0.335236
503 -0.942409 0.948493
504 -0.805966 0.675551
505 -0.578562 -0.470207
[452 rows x 2 columns]
0 24.0
1 21.6
2 34.7
3 33.4
4 36.2
...
501 22.4
502 20.6
503 23.9
504 22.0
505 11.9
Name: medv, Length: 452, dtype: float64
4.5. 分割訓練集與測試集
訓練集佔80%、測試集佔20%
1: # train_test_split 2: from sklearn.model_selection import train_test_split 3: X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state=5) 4: # 再用.shape看切出來的資料的長相(列, 欄) 5: print(X_train.shape) 6: print(X_test.shape) 7: print(Y_train.shape) 8: print(Y_test.shape)
(361, 2) (91, 2) (361,) (91,)
4.6. 建立模型
new出一個LinearRegression的物件後,用特徵變數的訓練資料和目標變數的訓練資料產生一個模型。接著將特徵變數的測試資料倒進這個新產生的模型當中,得到預測的目標變數資料1。
1: # Modeling 2: from sklearn.linear_model import LinearRegression 3: reg = LinearRegression()# 學習/訓練Fitting linear model 4: reg.fit(X_train,Y_train)
4.7. 測試效能
將這個預測的目標變數資料(預測結果)和目標變數的測試資料(真實結果)做R2-score:
1: # 預測結果Predicting using the linear model 2: reg.predict(X_test)# 真實結果:Y_test# 測試準確度: 3: print('R2:', reg.score(X_test, Y_test))
R2: 0.6048366146231109
得到的這個R2-score讓我們可以知道特徵變數對於目標變數的解釋程度為何,而越接近1代表越準確。這裡大約是60%,解釋程度尚可1。
4.7.1. 模型效能視覺化
把剛剛的預測的目標變數資料和測試的目標變數資料畫成散佈圖
1: # plotting the y_test vs y_pred 2: Y_pred = reg.predict(X_test) 3: plt.cla() 4: plt.tight_layout() 5: plt.figure(figsize=(10,8)) 6: 7: plt.scatter(Y_pred, Y_test) 8: plt.xlabel('Y_pred') 9: plt.ylabel('Y_test') 10: plt.savefig('images/boston-perf.png', dpi=300)
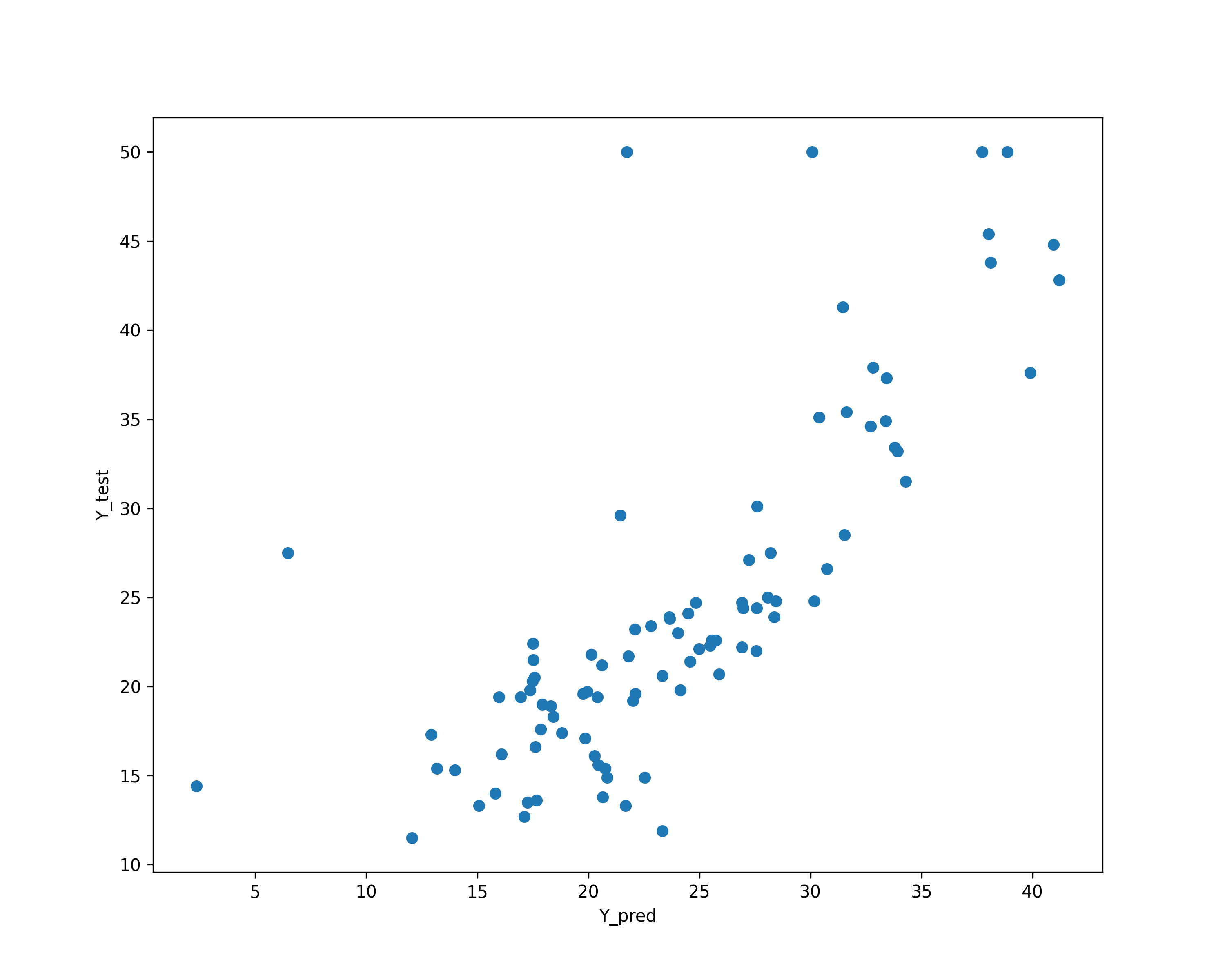
Figure 13: 預測結果與實際結果的散佈圖
4.8. 找出線性模型
由LinearRegression()找出線性模型的intercept和coefficient
1: print('intercept:',reg.intercept_) 2: print('coefficient::',reg.coef_) 3: print('lstat:',reg.coef_[0]) 4: print('rm:',reg.coef_[1])
intercept: 23.662167506495486 coefficient:: [-3.2284783 4.66331239] lstat: -3.228478297753095 rm: 4.663312387946355
線性模型為:\(medv=23.66 + -3.22 \times lstat + 4.66 \times rm + error\)
5. 關於迴歸模型的特徵選擇
在進行迴歸分析時,我們可以選擇不同的特徵來建立模型,這裡介紹兩種方法:
- 前向選擇法(Forward Selection)
- 後向選擇法(Backward Selection)
5.1. 前向選擇法(Forward Selection)
前向選擇法是一種逐步選擇特徵的方法,它從空模型開始,然後逐步添加特徵,直到達到某個標準為止。這種方法的優點是可以減少過擬合的風險,但是需要注意的是,如果特徵之間存在 多重共線性(Multicollinearity) ,則可能會導致模型不穩定。
5.2. 後向選擇法(Backward Selection)
後向選擇法是一種逐步刪除特徵的方法,它從包含所有特徵的模型開始,然後逐步刪除特徵,直到達到某個標準為止。這種方法的優點是可以減少過擬合的風險,但是需要注意的是,如果特徵之間存在多重共線性,則可能會導致模型不穩定。
5.3. 特徵選擇的注意事項
在進行特徵選擇時,需要注意以下幾點:
5.3.1. 特徵之間的相關性
特徵之間的相關性可能會導致模型不穩定,因此在進行特徵選擇時,需要注意特徵之間的相關性,避免選擇相關性較高的特徵。
以lstat, rm, indus, ptratio這四個特徵為例,我們可以使用 皮爾遜相關係數(Pearson Correlation) 來衡量 lstat 與 rm、indus、ptratio 的線性關係。
1: import seaborn as sns 2: import matplotlib.pyplot as plt 3: 4: # 計算 lstat 與其他變數的相關性 5: lstat_corr = housing[['lstat', 'rm', 'indus', 'ptratio']].corr() 6: 7: # 顯示相關係數表 8: print("lstat 與其他變數的相關性:") 9: print(lstat_corr) 10: 11: # 繪製相關係數熱圖 12: plt.figure(figsize=(8, 6)) 13: sns.heatmap(lstat_corr, annot=True, cmap="coolwarm", fmt=".2f") 14: plt.title("lstat correlation with other variables") 15: plt.savefig('images/lstat-corr.png', dpi=300) 16:
lstat 與其他變數的相關性:
lstat rm indus ptratio
lstat 1.000000 -0.607289 0.565402 0.303043
rm -0.607289 1.000000 -0.364895 -0.334164
indus 0.565402 -0.364895 1.000000 0.317336
ptratio 0.303043 -0.334164 0.317336 1.000000
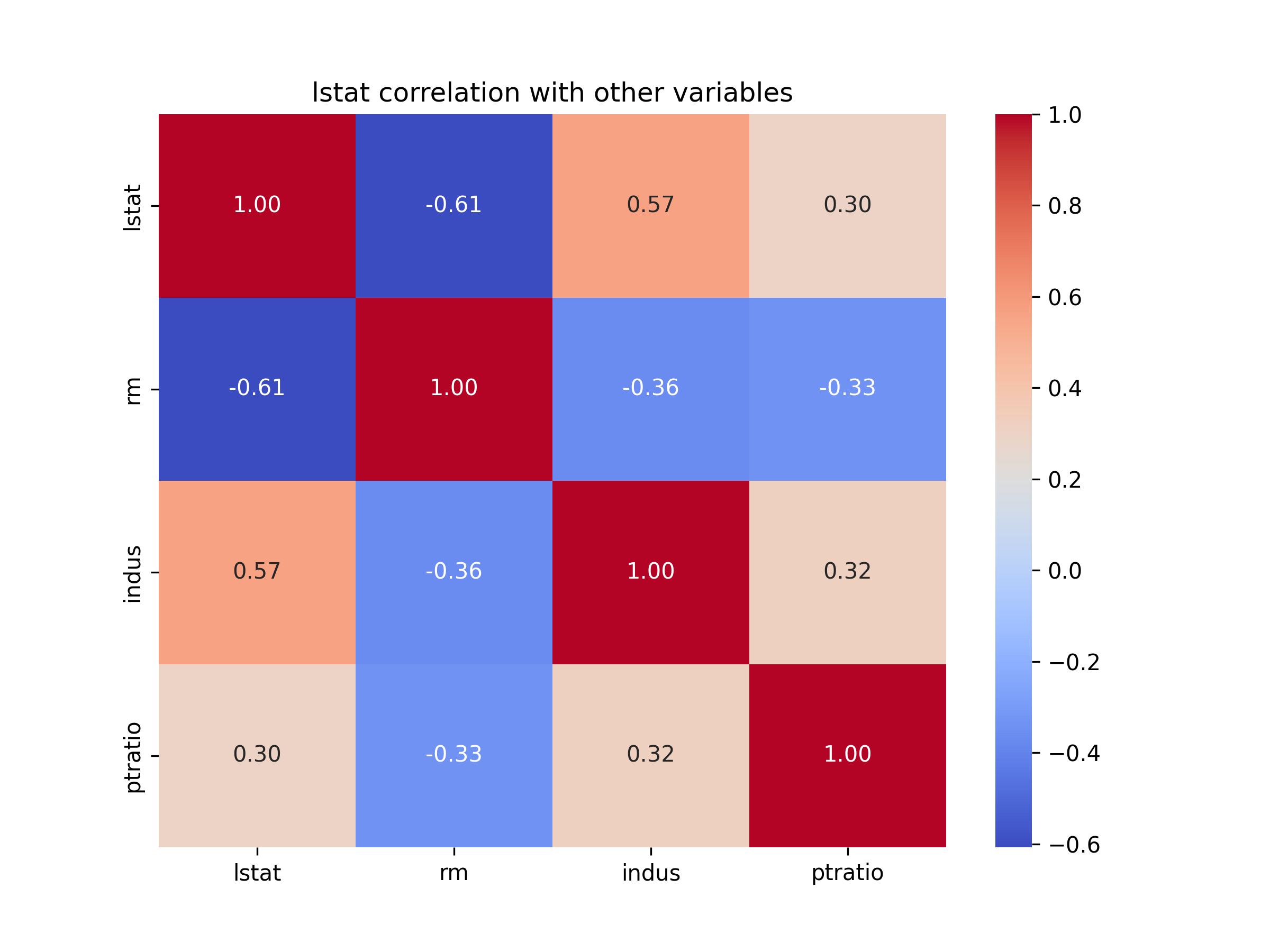
Figure 14: lstat 與其他變數的相關性
5.3.2. 如何解讀相關性?
相關係數範圍:-1(完全負相關)到 +1(完全正相關)
- |r| > 0.8:高度相關(可能有多重共線性)
- 0.5 < |r| < 0.8:中等相關(可能需要進一步檢查)
- |r| < 0.5:低相關(通常不會造成共線性問題)
5.3.3. 為什麼變數之間的共變(高相關性)會影響迴歸結果?
變數之間高共變影響迴歸模型
當兩個變數彼此高度相關時(例如 rm 和 lstat 相關性 -0.73):
這兩個變數都能解釋目標變數 MEDV(房價)。
但因為它們彼此也高度相關,回歸模型無法區分到底是哪個變數真正影響房價,所以模型可能會:
- 讓其中一個變數的迴歸係數變得極端大或極端小,以補償另一個變數。
- 讓其中一個變數的迴歸係數變得極端大或極端小,以補償另一個變數。
多重共線性會影響模型泛化能力
- 假設我們的模型發現: \(x_1\) (房屋面積)和 \(x_2\)(房間數)高度相關
- 由於數據集的特性,模型可能學到:
- \(x_1\)影響比較大,\(x_2\) 影響比較小
- 但換一組數據集時,模型可能學到 \(x_2\) 影響比較大,\(x_1\)影響比較小
- \(x_1\)影響比較大,\(x_2\) 影響比較小
這會導致:
- 在不同的測試集上,模型預測結果不穩定。
- 當我們遇到新數據時,模型的預測結果可能變化很大。
- 假設我們的模型發現: \(x_1\) (房屋面積)和 \(x_2\)(房間數)高度相關
5.3.4. 如何解決?
方法 1:刪除其中一個變數
如果 \(x_1\) 和 \(x_2\) 高度相關(相關係數 > 0.8),可以考慮刪除其中一個。例如:
- 刪除 \(x_2\)(房間數),只保留 \(x_1\)(房屋面積)。
- 選擇一個對 MEDV 影響更大的變數(透過 corr() 和 VIF 來選擇)。
方法 2:合併變數
有時候可以建立一個新變數,代表這些高度相關變數的組合資訊。例如:
- 用「每平方公尺的房間數」(\(x_2\) / \(x_1\) 來替代 \(x_1\) 和 \(x_2\),這樣就避免兩個變數的高度相關性。
方法 3:使用 Ridge Regression(L2 正則化)
- Ridge 迴歸會對回歸係數加上一個懲罰,使它們不會變得過大,從而減少共線性的影響。
- 適合當 VIF 在 5~10 之間的變數,因為它不會直接移除變數,而是調整其影響力。
方法 4:使用 PCA(主成分分析)降維
- 透過 PCA 將高度相關的變數轉換為不相關的新特徵(如 PC1、PC2)。
- 這樣可以讓回歸模型使用的變數之間不會有多重共線性問題。
5.4. 多重共線性(Multicollinearity)
多重共線性是指特徵之間存在高度相關性的情況,這種情況下,模型的參數估計可能會變得不穩定,並且可能會導致模型的預測能力下降。因此,在進行特徵選擇時,需要注意特徵之間的相關性,避免多重共線性的問題。
當我們檢查 lstat(低收入族群比例)與其他變數的相關性時,指的是 lstat 與 其餘三個變數 (rm, indus, ptratio) 的 共變關係(即相關係數, Correlation Coefficient)。
5.4.1. 檢查多重共線性(VIF, Variance Inflation Factor)
- 若兩個或多個變數之間的相關性過高,可能會影響迴歸模型的穩定性。
- VIF > 5 通常表示該變數與其他變數的相關性過高,應考慮移除。
1: import pandas as pd 2: import numpy as np 3: import seaborn as sns 4: import matplotlib.pyplot as plt 5: from sklearn.preprocessing import StandardScaler 6: from statsmodels.stats.outliers_influence import variance_inflation_factor 7: 8: # 讀取 Boston Housing 資料 9: housing = pd.read_csv('https://raw.githubusercontent.com/letranger/AI/gh-pages/Downloads/boston_housing.csv') 10: 11: # 目標變數 12: target_column = 'medv' 13: 14: # 計算相關係數 15: correlation_matrix = housing.corr() 16: 17: # 只顯示與目標變數的相關性 18: corr_target = correlation_matrix[target_column].drop(target_column).sort_values(ascending=False) 19: 20: # 設定相關性閾值(例如:0.4 以上為較強相關) 21: threshold = 0.4 22: selected_features = corr_target[abs(corr_target) > threshold].index.tolist() 23: 24: # 過濾後的特徵 25: filtered_data = housing[selected_features + [target_column]] 26: 27: # 顯示相關性較高的特徵 28: print("與目標變數相關性較高的特徵:") 29: print(filtered_data.head()) 30: 31: # 畫出相關係數熱圖 32: plt.figure(figsize=(10, 6)) 33: sns.heatmap(filtered_data.corr(), annot=True, cmap="coolwarm", fmt=".2f") 34: plt.title("The correlation heatmap of features related to MEDV") 35: plt.savefig('images/boston-heatmap.png', dpi=300) 36: 37: # 計算 VIF(變異膨脹因子) 38: X = housing[selected_features] 39: #vif_data = pd.DataFrame() 40: #vif_data["Feature"] = X.columns 41: #vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])] 42: 43: # 建立 VIF DataFrame(簡易版) 44: vif_data = pd.DataFrame() 45: vif_data["Feature"] = X.columns # 記錄變數名稱 46: vif_values = [] # 存放每個變數的 VIF 值 47: 48: # 使用 for 迴圈逐個變數計算 VIF 49: for i in range(X.shape[1]): 50: vif = variance_inflation_factor(X.values, i) # 計算 VIF 51: vif_values.append(vif) # 加入列表 52: 53: # 將 VIF 值存入 DataFrame 54: vif_data["VIF"] = vif_values 55: 56: # 顯示 VIF 結果 57: print("\n變異膨脹因子(VIF)檢測結果:") 58: print(vif_data)
與目標變數相關性較高的特徵:
rm indus ptratio lstat medv
0 6.575 2.31 15.3 4.98 24.0
1 6.421 7.07 17.8 9.14 21.6
2 7.185 7.07 17.8 4.03 34.7
3 6.998 2.18 18.7 2.94 33.4
4 7.147 2.18 18.7 5.33 36.2
變異膨脹因子(VIF)檢測結果:
Feature VIF
0 rm 4.022386
1 indus 4.063422
2 ptratio 3.545233
3 lstat 5.000509
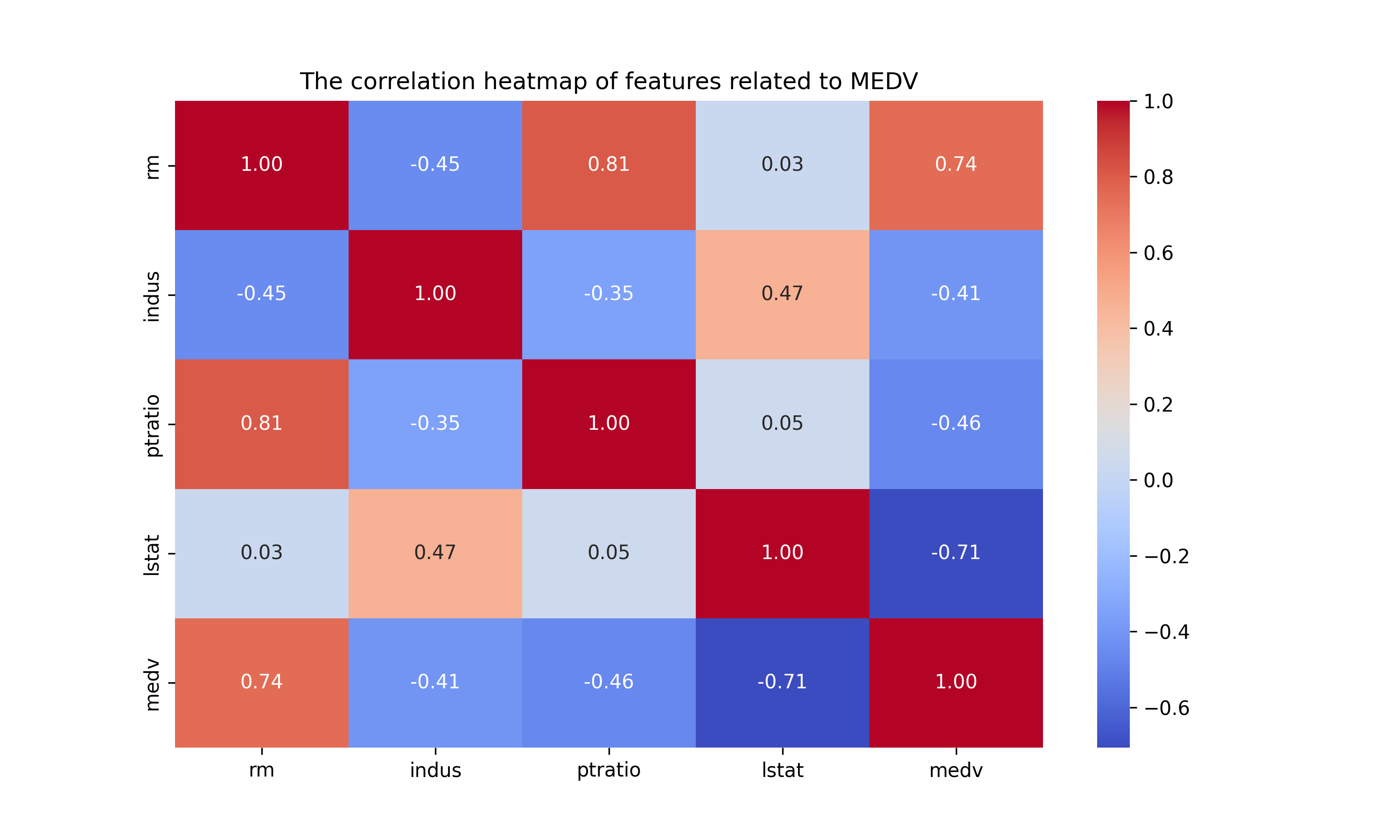
Figure 15: 與MEDV相關性較高的特徵熱圖
5.4.2. 如何判斷 VIF 是否過高?
- VIF < 5:通常可以接受,代表該變數與其他變數的相關性不高。
- VIF 5~10:表示有些許多重共線性,建議進一步檢查,但不一定要刪除變數。
- VIF > 10:代表嚴重的多重共線性,應該考慮移除或合併變數。
6. 課堂練習 TNFSH
6.1. 練習一:用 scikit-learn 完成一次迴歸
以下是 10 位同學的每週讀書時數與期末考成績資料。請完成以下任務:
- 將資料畫成散佈圖
- 用
LinearRegression建立迴歸模型 - 印出模型的斜率與截距
- 預測每週讀書 8 小時和 15 小時的同學,期末考大約幾分?
- 畫出迴歸線
- 計算模型的 R² 分數
1: import numpy as np 2: import matplotlib.pyplot as plt 3: from sklearn.linear_model import LinearRegression 4: 5: # --- 資料(直接內嵌,不需下載)--- 6: hours = np.array([2, 3, 5, 6, 7, 8, 10, 12, 14, 16]).reshape(-1, 1) # 每週讀書時數 7: scores = np.array([35, 42, 50, 55, 60, 62, 72, 78, 85, 90]) # 期末考成績 8: 9: # 1. 畫散佈圖 10: 11: # 2. 建立模型並訓練 12: 13: # 3. 印出斜率與截距 14: 15: # 4. 預測讀書 8 小時和 15 小時的成績 16: 17: # 5. 畫出迴歸線 18: 19: # 6. 計算 R² 分數
6.2. 練習二:單變數 vs 多變數迴歸比較
使用波士頓房價資料集,比較「只用 1 個特徵」與「用多個特徵」建模的預測效果差異。
任務:
- 分別用以下兩種方式建立迴歸模型:
- 模型 A:只用 =lstat=(低收入人口比例)一個特徵
- 模型 B:用
lstat,rm,ptratio,indus四個特徵
- 模型 A:只用 =lstat=(低收入人口比例)一個特徵
- 比較兩個模型的 R² 分數,觀察特徵數量對預測力的影響
- 思考:是不是特徵越多就越好?
1: import pandas as pd 2: from sklearn.linear_model import LinearRegression 3: from sklearn.model_selection import train_test_split 4: 5: # 下載資料 6: housing = pd.read_csv('https://raw.githubusercontent.com/letranger/AI/gh-pages/Downloads/boston_housing.csv') 7: housing.dropna(inplace=True) 8: 9: y = housing['medv'] 10: 11: # 模型 A:只用 lstat 12: 13: # 模型 B:用 lstat, rm, ptratio, indus 14: 15: # 比較兩個模型的 R² 分數
7. [作業] AI 算命師養成計畫:預測同學的期末考成績 TNFSH
劇情設定
恭喜你被學校旁邊新開的「AI 算命攤」錄取為實習生了!攤主王大媽表示:「我們這裡不擲筊、不抽籤,我們用 迴歸分析 預測命運。」
你的第一個任務:根據 424 位學生的歷史資料,建立一個「期末考成績預測模型」。
王大媽語重心長地說:「預測得準,你就能提前知道誰該被約談;預測不準的話——你自己也該被約談了。」
7.1. 案件資料
- 線上資料: https://letranger.github.io/AI/Downloads/PythonScores.csv
王大媽提供了 424 位學生的機密檔案,每筆記錄包含:
欄位名稱 說明 備註 id 學號 不能用來預測,但可以用來對質 class 平時成績 代表「有沒有乖乖出現在教室」 task 作業成績 代表「有沒有乖乖寫作業(或乖乖抄同學的)」 mid 期中考成績 代表「至少有沒有在期中醒過來」 final 期末考成績 你要預測的目標:命運的審判
7.2. 任務
身為一個有專業素養的 AI 算命師,請完成以下修煉:
- *資料清洗*:部分學生的期中、期末考欄位有缺失值(就是那些考試當天「剛好」生病的同學)。請將缺失值填入 0 分——是的,缺考就是零分,人生本來就是這麼殘酷。
- *資料觀察*:畫出所有特徵資料的分佈狀況(直方圖)。看看平時成績是不是大家都差不多,而期末考是不是呈現「雙峰分佈」——一群學霸、一群⋯⋯嗯。
- *相關性分析*:用視覺化方式(如 heatmap)呈現所有分數之間的相關性。猜猜看:平時成績、作業成績、期中考,哪個最能預測期末考?(如果答案是「都不太行」,那就代表人生充滿驚喜。)
- *訓練模型*:將資料分成訓練集(70%)和測試集(30%),用
LinearRegression建立迴歸模型。 - *評估模型*:你可以自行選擇要用幾個特徵值來預測。用測試集計算 R² 分數,看看你的模型到底是「半仙」還是「半殘」。
- *揭曉天機*:列出你的模型方程式。這就是你的「算命公式」——以後看到一個同學的平時成績和期中考分數,你就能預言他的期末考命運了。
*加分挑戰(選做)*:試試看只用「期中考」一個特徵預測期末考,再用「全部三個特徵」預測。哪個模型比較準?為什麼多了資訊不一定更準確?(提示:想想那些平時 100 分但期末 0 分的奇葩同學對模型造成了什麼影響。)
8. [卜聖卦活動2]以迴歸預測成績 TNFSH
8.1. 資料集
- 10Asub1: 高一上英文
- 10Asub2: 高一上數學
- 10Asub3: 高一上國文
- 10BSub1: 高一下英文
- 10BSub2: 高一下數學
- 10BSub3: 高一下國文
- 11ASub1: 高二上英文
- 11ASub2: 高二上數學
- 11ASub3: 高二上國文
- 12ASub1: 高三上英文
- 12ASub2: 高三上數學
- 12ASub3: 高三上國文
- 12BSub1: 高三下英文
- 12BSub2: 高三下數學
- 12BSub3: 高三下國文
- TestNG3: (學測)自然組國英數三科
- TestSG3: (學測)社會組國英數三科
1: import pandas as pd 2: 3: df = pd.read_csv('https://raw.githubusercontent.com/letranger/AI/refs/heads/gh-pages/3yScTest.csv') 4: print(df.columns) 5: print(df.head())
Index(['10ASub1', '10ASub2', '10ASub3', '10BSub1', '10BSub2', '10BSub3',
'11ASub1', '11ASub2', '11ASub3', '11BSub1', '11BSub2', '11BSub3',
'12ASub1', '12ASub2', '12ASub3', '12BSub1', '12BSub2', '12BSub3',
'TestNG3', 'TestSG3'],
dtype='object')
10ASub1 10ASub2 10ASub3 10BSub1 ... 12BSub2 12BSub3 TestNG3 TestSG3
0 31 38 61 34 ... 6.0 2.0 15 23
1 58 49 63 50 ... 1.0 2.0 29 41
2 32 43 68 29 ... 25.0 87.0 20 32
3 55 46 74 56 ... 27.0 59.0 34 41
4 79 74 82 75 ... 31.0 86.0 40 47
[5 rows x 20 columns]
8.2. 任務:
- 預估二下英文科成績
- 預估二下數學科成績
- 預估二下國文科成績
- 預估學測成績