Activation Function

Table of Contents

Hits

1. 簡介

在神經網路中，有一個非常重要的元件叫做 Activation Function（啟動函數）。這個詞的中文翻譯有很多版本，常見的包括：

  • 啟動函數
  • 激勵函數
  • 激發函數
  • 激活函數（常見於中國用語）

要了解Activation Function在AI模型中所扮演的角色，我們可以這樣理解：它負責判斷一個神經元接收到的訊號值不值得被「啟動」留下來，或者該被「關閉」（等於沒貢獻）。

Activation Function 是讓神經網路真正「有智慧」的關鍵之一，它賦予神經元選擇性與彈性，不只是單純的數學加總而已。一個神經元的計算流程大致如下：

  1. 神經元接收到輸入值，乘上各自對應的權重（weights）
  2. 計算加總後的結果
  3. 經由 Activation Function 判斷這個訊號是否強大到需要被「啟動」
    • 過了門檻（threshold）：輸出變為 1（或接近 1）
    • 沒過門檻：輸出變為 0（或接近 0）

1.1. 線性模型的限制與啟動函數的必要性

如果一個神經網路由沒有使用 Activation Function 的感知器（Perceptron）所組成，那它本質上只是個線性模型。線性模型無法處理複雜的非線性問題。

為了解釋這個概念，我們來看看底下這個堆疊兩層感知器的例子，這個例子中我們假設有兩個輸入特徵 \(x_1\) 和 \(x_2\)，沒有使用 Activation Function，為了讓概念更清楚，我們也暫時忽略偏移值(bias) \(b\)，只看權重\(w\)與輸入\(x\)。 沒有啟動函數的感知器只能計算出一個線性組合：

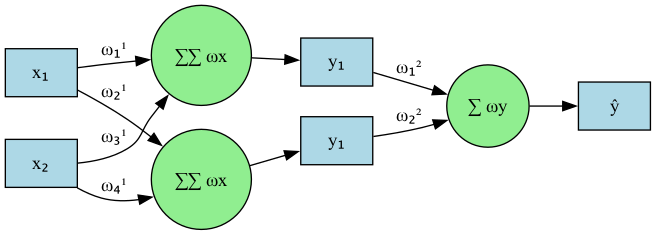
MLP-AC.png

Figure 1: Stacked perceptrons

其中每層的運算如下：

\begin{align} y_1 = w_1^1x_1 + w_2^1x_2 \\ y_2 = w_3^1x_1 + w_4^1x_2 \\ \hat{y} = w_1^2y_1 + w_2^2y_2 \end{align}

若將 \(y_1\) 與 \(y_2\) 代入 \(\hat{y}\) 中： \[\hat{y} = w_1^2(w_1^1x_1 + w_2^1x_2) + w_2^2(w_3^1x_1 + w_4^1x_2)\] 整理後： \[\hat{y} = (w_1^1w_1^2 + w_2^1w_2^2)x_1 + (w_3^1w_1^2 + w_4^1w_2^2)x_2\]

這表示：

  • 雖然我們堆了兩層，但最後結果仍是輸入變數 \(x_1, x_2\) 的線性組合。
  • 堆再多層都沒有用，本質上還是單一感知器可以做的事。

啟動函數最重要的功能在於引入神經網路非線性，因為若未加入啟動函數，卷積層與全連接層只是單純的線性運算，只是將上層的數據經過線性地組合成下層數據而已，對於線性不可分的問題仍然是無解的1。

舉個常見的例子，如果輸入的資料如圖2(這是互斥或閘XOR的例子)，紅點(B)與藍點(A)分別是兩種不同的類別，我們的目標就是利用一條直線將兩類別切開，但實際上根本辦不到，這就是線性模型的極限。

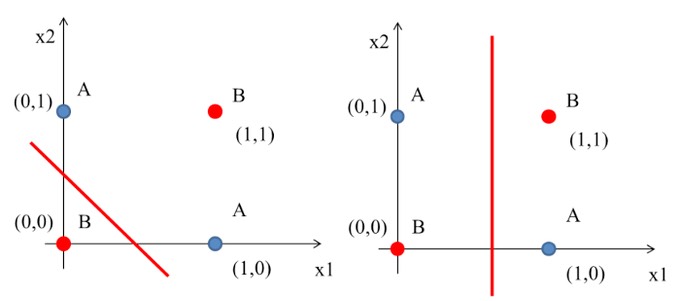
2021-05-24_14-18-51.jpg

Figure 2: XOR Gate Solution ideas

如果沒有Activation Function（啟動函數）：

  • 卷積層與全連接層只是簡單的線性映射
  • 模型無法處理非線性可分問題
  • 不論疊幾層，都只是「線性換湯不換藥」

2. 常見的啟動函數（Activation Functions）

在神經網路中，啟動函數的主要目的在於引入非線性，使得模型能處理複雜、非線性可分的問題。以下介紹幾種常見的啟動函數：

2.1. Step function（階梯函數）

Step 函數是最早期的啟動函數之一。它的規則很簡單：

  • 如果輸入大於 0，輸出為 1
  • 否則輸出為 0

這裡是它的數學表示式（見公式 \eqref{org427e9c1}）與對應圖形（圖3)：

\begin{equation} \label{org427e9c1} h(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x\leq 0 \end{cases} \end{equation} 
 1: import numpy as np               # 匯入 NumPy，數值運算的瑞士刀
 2: import matplotlib.pylab as plt   # 匯入 Matplotlib，專門畫圖用的
 3: 
 4: # 定義階梯函數：輸入大於 0 就輸出 1，否則輸出 0
 5: # 就像考試及格與不及格，沒有中間地帶，非黑即白
 6: def step_function(x):
 7:     # x>0 會產生 True/False 陣列，再用 dtype=int 把 True 變 1、False 變 0
 8:     return np.array(x>0, dtype=int)
 9: 
10: x = np.arange(-5.0, 5.0, 0.1)   # 產生從 -5 到 5（不含）的數列，間隔 0.1
11: y = step_function(x)             # 把每個 x 值丟進階梯函數，得到對應的 y 值
12: plt.figure(figsize=(4,3))        # 建立一張 4x3 吋的畫布
13: plt.plot(x, y)                   # 畫出 x 和 y 的折線圖
14: plt.ylim(-0.1, 1.1)             # 設定 y 軸範圍，留一點空間比較好看
15: plt.savefig("images/stepFuncPlot.png")  # 把圖存成 PNG 檔
16: return "images/stepFuncPlot.png"

stepFuncPlot.png

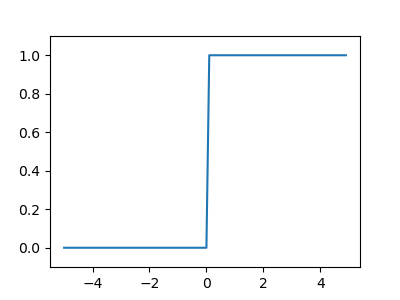
Figure 3: 階梯函數圖

Step 函數的優點在於：

  • 簡單易懂：其邏輯非常直觀，容易實作。
  • 二元輸出：輸出只有 0 或 1，適合二元分類問題。

至於其缺點則包括：

  • 不連續：在 0 處不連續，這會導致梯度下降法無法有效學習。
  • 無法處理多類別問題：只能處理二元分類，無法擴展到多類別問題。

2.2. Sigmoid

Sigmoid 函數能將輸入轉換為 0 到 1 之間的實數，曲線平滑，常用於輸出表示機率。公式\eqref{org4c55411}即為 sigmoid 函數(sigmoid function)，其中的\(exp(-x)\)代表\(e^{-x}\)，\(e\)為納皮爾常數(Napier’s constant)，這是一個值為2.71828的實數。

\begin{equation} \label{org4c55411} h(x) = \frac{1}{1+exp(-x)} = \frac{1}{1+e^{-x}} \end{equation}

sigmoid 函數的 python 實作如下所述，而其圖形結果為平滑曲線(圖4)，針對輸入產生連續性的輸出，但仍與階梯函數相同，以 0 為界線，這種平滑度對於神經網路有相當重要的意義。此外，step function只能回傳 0 或 1，而 sigmoid 函數可以回傳實數。 

 1: import numpy as np               # 匯入 NumPy
 2: import matplotlib.pylab as plt   # 匯入 Matplotlib 畫圖套件
 3: 
 4: # 定義 Sigmoid 函數：把任意數字「壓縮」到 0～1 之間
 5: # 想像成一個溫柔版的階梯函數，不再是非黑即白，而是漸層過渡
 6: def sigmoid(x):
 7:     # 公式：1 / (1 + e^(-x))，e 是自然常數（大約 2.718）
 8:     return 1 / (1 + np.exp(-x))
 9: 
10: x = np.arange(-5.0, 5.0, 0.1)   # 產生 -5 到 5 的數列，間隔 0.1
11: y = sigmoid(x)                   # 計算每個 x 對應的 sigmoid 值
12: print(y)                         # 印出 y 值，看看 sigmoid 的輸出長什麼樣
13: plt.figure(figsize=(4,3))        # 建立 4x3 吋的畫布
14: plt.plot(x, y)                   # 畫出平滑的 S 形曲線（sigmoid 的招牌造型）
15: plt.ylim(-0.1, 1.1)             # y 軸範圍設為 -0.1 到 1.1
16: plt.savefig("images/sigmoidplot2.png")  # 存圖
17: return "images/sigmoidplot2.png"

sigmoidplot2.png

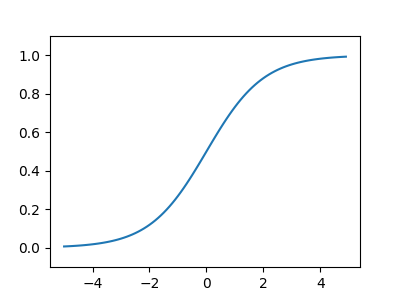
Figure 4: sigmoid 函數圖

Sigmoid函數的特點：

  • 非線性、連續可導
  • 輸出範圍：(0, 1)
  • 適合表示「機率」

至於其缺點則是容易出現「梯度消失(vanishing gradient)」問題，這是因為在極端輸入下，sigmoid 函數的導數趨近於 0，這會導致梯度下降法學習速度變慢。

2.3. ReLU

雖然 sigmoid 函數很早就應用於神經網路中，但目前最常使用的啟動函數則為 ReLU（Rectified Linear Unit）。ReLU的定義很簡單：若輸入超過 0，則直接輸出；若輸入小於 0，則輸出 0，如公式\eqref{org8c30dee}所示：

\begin{equation} \label{org8c30dee} h(x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x\leq 0 \end{cases} \end{equation}

或簡寫為： \[h(x) = max(0,x)\]

至於其函數圖形則如圖5所示。 

 1: import numpy as np               # 匯入 NumPy
 2: import matplotlib.pylab as plt   # 匯入 Matplotlib 畫圖套件
 3: 
 4: # 定義 ReLU 函數：正數就原封不動放行，負數一律歸零
 5: # 簡單粗暴但超有效，目前神經網路界的當紅炸子雞
 6: def relu(x):
 7:     # np.maximum(0, x) 會逐元素比較，取 0 和 x 中較大的那個
 8:     return np.maximum(0, x)
 9: 
10: x = np.arange(-5.0, 5.0, 0.1)   # 產生 -5 到 5 的數列
11: y = relu(x)                      # 計算 ReLU 輸出：負的全砍，正的留下
12: print(y)                         # 印出看看結果
13: plt.figure(figsize=(4,3))        # 開一張 4x3 吋的畫布
14: plt.plot(x, y)                   # 畫出來會是一條從原點開始往右上的直線
15: plt.ylim(-0.5, 5)               # y 軸範圍 -0.5 到 5
16: plt.savefig("images/ReLUPlot.png")  # 存圖
17: return "images/ReLUPlot.png"

ReLUPlot.png

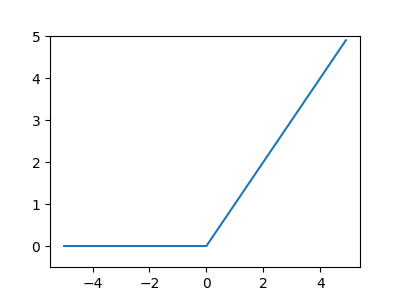
Figure 5: ReLU 函數圖

ReLU函數的特點：

  • 非線性但非常簡單
  • 計算快，收斂速度快
  • 輸出範圍：[0, ∞)
  • 常用於隱藏層

至於其缺點則是容易出現：輸入為負時會完全阻斷梯度（“死亡 ReLU”）。這是什麼意思呢？

想像我們有一個神經元，就像一顆燈泡，輸入電流 xx 後才會亮（有輸出），但如果輸入是負的，它就不亮（輸出是 0）。這似乎也沒什麼問題對吧，但重點是：

  • 訓練神經網路的過程中，我們會根據輸出來調整權重 （這個調整的方式叫做「反向傳播」需要用到函數的導數）。
  • 而，ReLU 的導數在輸入小於等於 0 時是 0！

也就是說：

  • 當一個神經元的輸入長期為負
  • 它的輸出永遠是 0
  • 而且因為導數也是 0，訓練的時候就完全無法更新它的權重

這就像一顆「死掉」的燈泡，你再怎麼訓練，它都不會亮、不會改，這就是所謂的：死亡 ReLU（Dead ReLU）

總之，ReLU 很快、效果好，但要小心它「對負數完全不回應」的這項特性。這意味著：如果某些神經元在一開始就輸入都是負數，很可能整場訓練它都不會作用。

現在，你有沒有了解為什麼我們在進行資料預處理時，常常會將數據標準化（normalization）或正規化（normalization）了？

2.4. Softmax

Softmax 函數主要用在輸出層，適合多分類問題。它的輸出：

  • 是 0 到 1 之間的實數
  • 並且總和為 1

有什麼場景是很多小數總和為1的？答案是：「機率分布」

2.4.1. 特色

softmax 的輸出為介於 0 到 1 間的實數，此外，其輸出總和為 1，這個性質使得 softmax 函數的輸出也可解釋為「機率」。例如，前節程式碼的輸出結果為[0.01821127 0.24519181 0.73659691]，從以機率的角度我們可以說：分類的結果有 1.8%的機率為第 0 類；有 24.52%的機率為第 1 類；有 73.66%的機率為第 2 類。換言之，使用 softmax 函數可以針對問題提出對應的機率。 softmax 函數的另一個特色是其輸出結果仍保持與輸入訊息一致的大小關係，這是因為指數函數\(y=exp(x)\)為單調函數。一般而言，神經網路會把輸出最大神經元的類別當作辨識結果，然而，因為 softmax 不影響大小順序，所以一般會省略 softmax 函數。

輸出層的節點數量取決於要解決的問題，例如，如果要解決的問題為「判斷一個手寫數字的結果」，則輸出層會有 10 個節點(分別代表 0~9)，而輸出訊息最大的結點則為最有可能的答案類別。

2.4.2. 公式

\begin{equation} \label{org7791ae0} y_k = \frac{exp(a_k)}{\sum_{i=1}^{n}exp(a_i)} \end{equation}

2.4.3. 實作

 1: import numpy as np  # 匯入 NumPy
 2: 
 3: # 定義 Softmax 函數：把一堆分數轉換成「機率分布」
 4: # 輸出值都在 0～1 之間，而且全部加起來剛好等於 1
 5: # 最適合用在多分類的輸出層，像是判斷手寫數字是 0～9 哪一個
 6: def softmax(a):
 7:     # 先減去最大值再做指數運算，避免 e 的次方爆掉（數字太大電腦會崩潰）
 8:     exp_a = np.exp(a - np.max(a))
 9:     # 算出所有指數值的總和，等一下要拿來當分母
10:     sum_exp_a = np.sum(exp_a)
11:     # 每個指數值除以總和，就得到機率了（加起來一定是 1）
12:     y = exp_a / sum_exp_a
13:     return(y)
14: 
15: a = np.array([0.3, 2.9, 4.0])   # 假設神經網路最後一層輸出了三個值
16: print(softmax(a))                # 印出 softmax 轉換後的機率分布

[0.01821127 0.24519181 0.73659691]

Footnotes:

1

CNN筆記 - 啟動函數 (Activation Function)與特徵轉換 (Feature Transform)

Author: Yung-Chin Yen

Created: 2026-04-15 Wed 20:56