非監督式學習
Table of Contents
1. 非監督式學習
Figure 1: AI, Machine Learning與Deep Learning
1.1. 目的
非監督式學習接收未被標記的數據,並通過演算法根據資料的基礎結構(如常見的模式、特色、或是其他因素)將數據分類,而非 做出預測 。例如:
- 將網站訪客進行分類: 性別、喜好、上網時段
將一堆照片依類型分類: cat、automobile、truck、frog、ship…
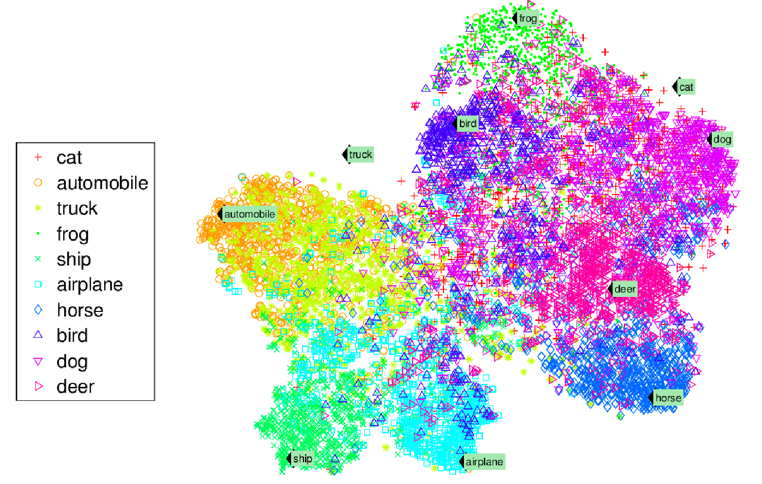
Figure 2: 照片分類
異常檢測(Anamaly Detection): 例如,找出不尋常的信用卡交易以防止詐騙、找出製程中有缺陷的產品、將資料組中的離群值挑出來再傳給另一個演算法
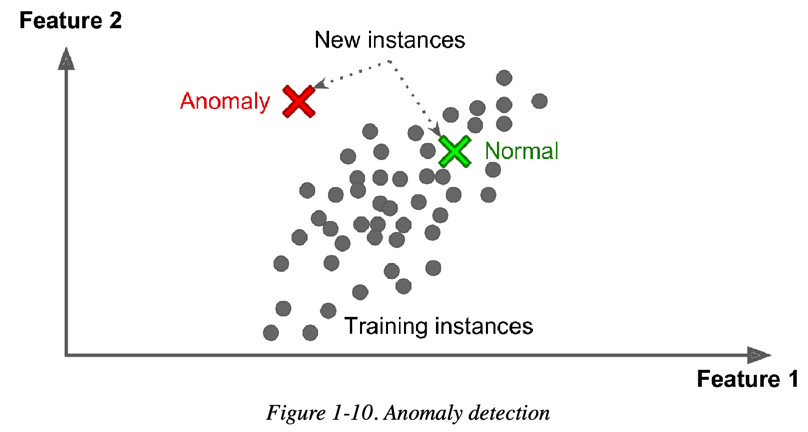
Figure 3: Novelty Detection
1.2. 非監督式學習的常見演算法
為了讓相近的資料可以聚集在一起,通常還是會將資料的特徵值數值化,再透過計算資料間的「距離」進行分群,在此常以「歐幾里得距離」為計算方式。以下為幾個主要任務與對應演算法:
1.2.1. 分群(clustering)
為了讓相近的資料聚集在一起,通常需先將資料的特徵值數值化,再透過計算資料間的「距離」來進行分群。常使用歐幾里得距離(Euclidean distance)。常見演算法:
- K-Means:以 K 個中心點將資料分為 K 群,並反覆調整以最小化群內誤差平方和(SSE)。
- DBSCAN:基於密度的分群演算法,可辨識任意形狀的群組並標記離群點。
- 階層式分群分析(Hierarchical Cluster Analysis, HCA):逐步合併或拆分群組形成層級樹狀結構。
1.2.2. 異常檢測與新穎檢測(Anomaly & Novelty Detection)
從資料中找出偏離主要分布的樣本,常應用於欺詐偵測、工業監控等。常見方法:
- One-class SVM:使用支持向量機學習正常資料的邊界,用以識別異常點。
- 孤立森林(Isolation Forest):利用隨機樹結構將異常點快速分離,效率高且適用高維資料。
1.2.3. 降維
將高維資料投影至低維空間,以利視覺化、運算效率提升或雜訊過濾。可分為兩大類:
線性投影(Linear Projection)
將資料進行線性轉換,保留最大變異性或主成分。
- 主成分分析(Principal component analysis, PCA)
將資料投影到保留最多變異量的方向(主成分)上。常見變形:
- Mini-batch PCA / Incremental PCA:適合大量資料分批處理
- Kernel PCA:加入核函數進行非線性降維
- Sparse PCA:產生稀疏主成分以提升可解釋性
- 奇異值分解(Singular value decomposition, SVD)
將原始矩陣分解為秩(rank)較小的矩陣乘積,用來壓縮或近似原矩陣,得原來的矩陣可以使用擁有較小的秩的矩陣所組成的線性組合來表示。常用於推薦系統、LDA、語意分析等領域。
- 隨機投影(Random projection)
將高維資料以隨機矩陣映射到低維空間,且大致保留資料之間的距離關係。可以使用隨機高斯矩陣(random Gaussian matrix)或隨機稀疏矩陣(random sparse matrix)來實現。可使用:
- 隨機高斯矩陣(random Gaussian matrix)
- 隨機稀疏矩陣(random sparse matrix)
- principal component analysis(主成分分析)
- singular value decomposition(奇異值分解)
- random projection(隨機投影)
非線性降維(Nonlinear Dimensionality Reduction)
假設資料分布於低維流形(manifold)上,透過學習鄰近關係進行嵌入。分為幾個常見方法族群:
- 流形學習(Manifold learning)
- Isomap: 透過**近鄰之間的捷徑距離(geodesic distance)**建立全局流形結構的低維表示。是 MDS(多維尺度轉換)的延伸。
- t-SNE(t-distributed Stochastic Neighbor Embedding): 將高維資料嵌入至 2D 或 3D 空間,強調保留鄰近點關係。非常適合視覺化高維資料,如詞向量、圖像特徵等。
- 多維尺度轉換(Multidimensional Scaling, MDS): 依據樣本間距離將資料配置於低維空間,使低維中的距離盡可能與高維中相似。
- 局部線性嵌入(Locally Linear Embedding, LLE): 假設每個點可由其鄰居線性重建,透過這些重建權重學習低維嵌入。
- 詞典學習(Dictionary Learning): 尋找一組稀疏基底來表示資料,可用於特徵提取與壓縮。
- 隨機樹嵌入(Random Trees Embedding): 使用隨機樹(例如隨機森林)建立非線性轉換,以獲得資料的新表徵。
- 獨立成分分析(Independent Component Analysis, ICA): 與 PCA 相對,將資料分解為統計上彼此獨立的成分,常用於信號分離。
- 核方法(Kernel-based Methods)
將資料映射到高維特徵空間,再進行線性降維(如 PCA):
- Kernel PCA(核主成分分析): 加入核技巧使 PCA 能捕捉非線性結構
- Kernel LDA(核線性判別分析): 非線性版本的線性判別分析
- 神經網路類降維(Neural network-based)
透過神經網路結構學習低維表示:
- Autoencoder(自編碼器): 一種非監督式神經網路,將資料壓縮再還原,潛在層即為降維表示
- Variational Autoencoder(VAE): 在 autoencoder 架構中加入機率分佈與正規化
- Parametric t-SNE:結合神經網路對 t-SNE 進行擬合,支援新資料投影
- 其他統計或圖論導向方法
- UMAP(Uniform Manifold Approximation and Projection):兼顧局部與全局結構,速度快,近年來熱門視覺化方法
- Diffusion Maps、Spectral Embedding 等:使用鄰接圖和特徵值分解學習嵌入
2. K-Means Clustering
- 先來這裡(K-Means Clustering Demo)試一下什麼是K-Means Cluestering。
- 「分群」的概念簡單來說就是將相近的資料彼此分在同一群體。
- K-means演算法:將n個點劃分到K個聚落中,如此一來每個點都屬於離其最近的聚落中心所對應之聚落,以之作為分群的標準。
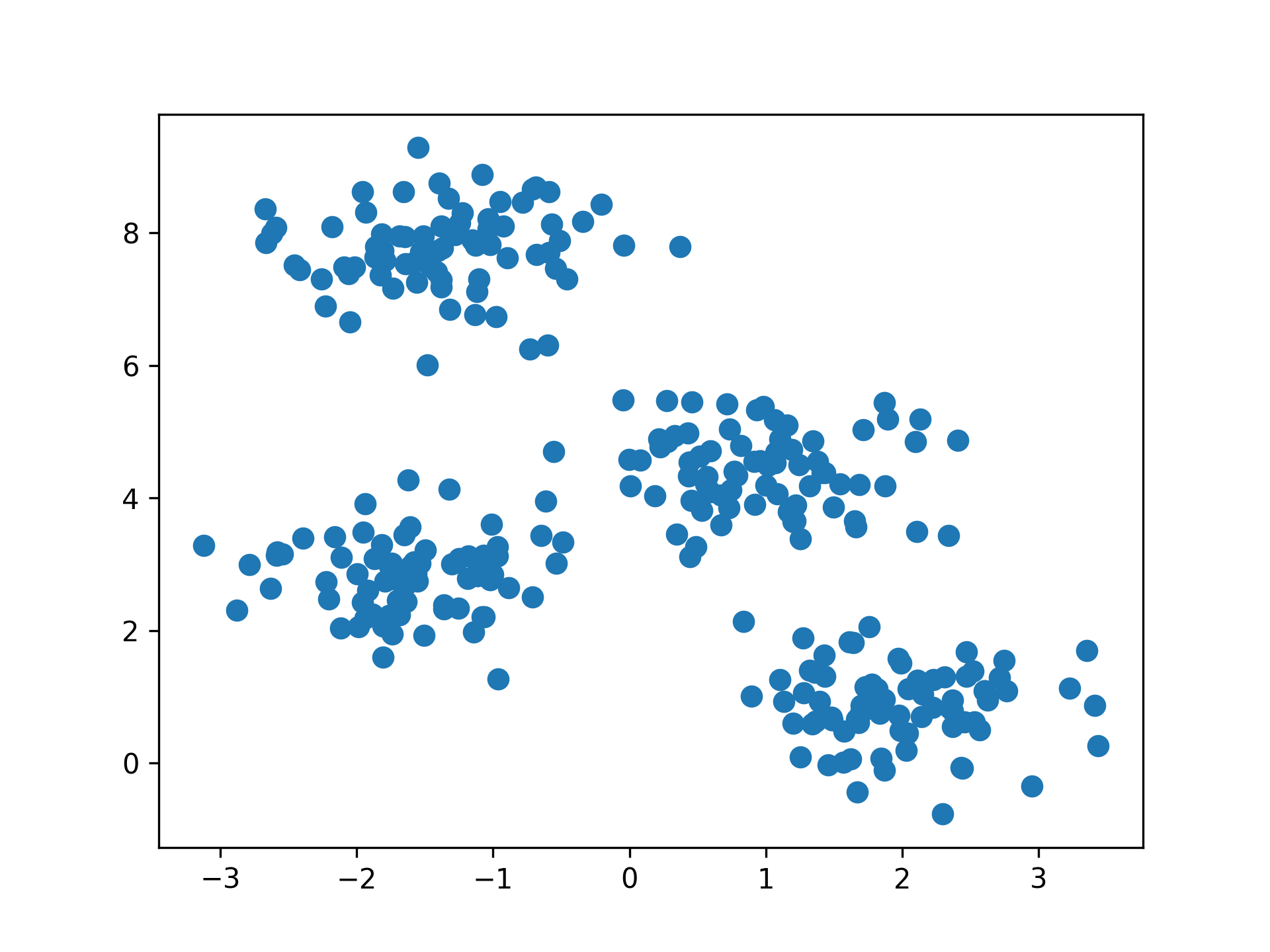
Figure 4: scikit-learn blobs
2.1. K-Means原理
八張未標註動物名稱(標籤)的照片,每張照片有兩個特徵值
/2024-02-10_20-19-55_2024-02-10_20-19-45.png)
Figure 5: 資料庫樣本
八張照片的特徵分佈如下
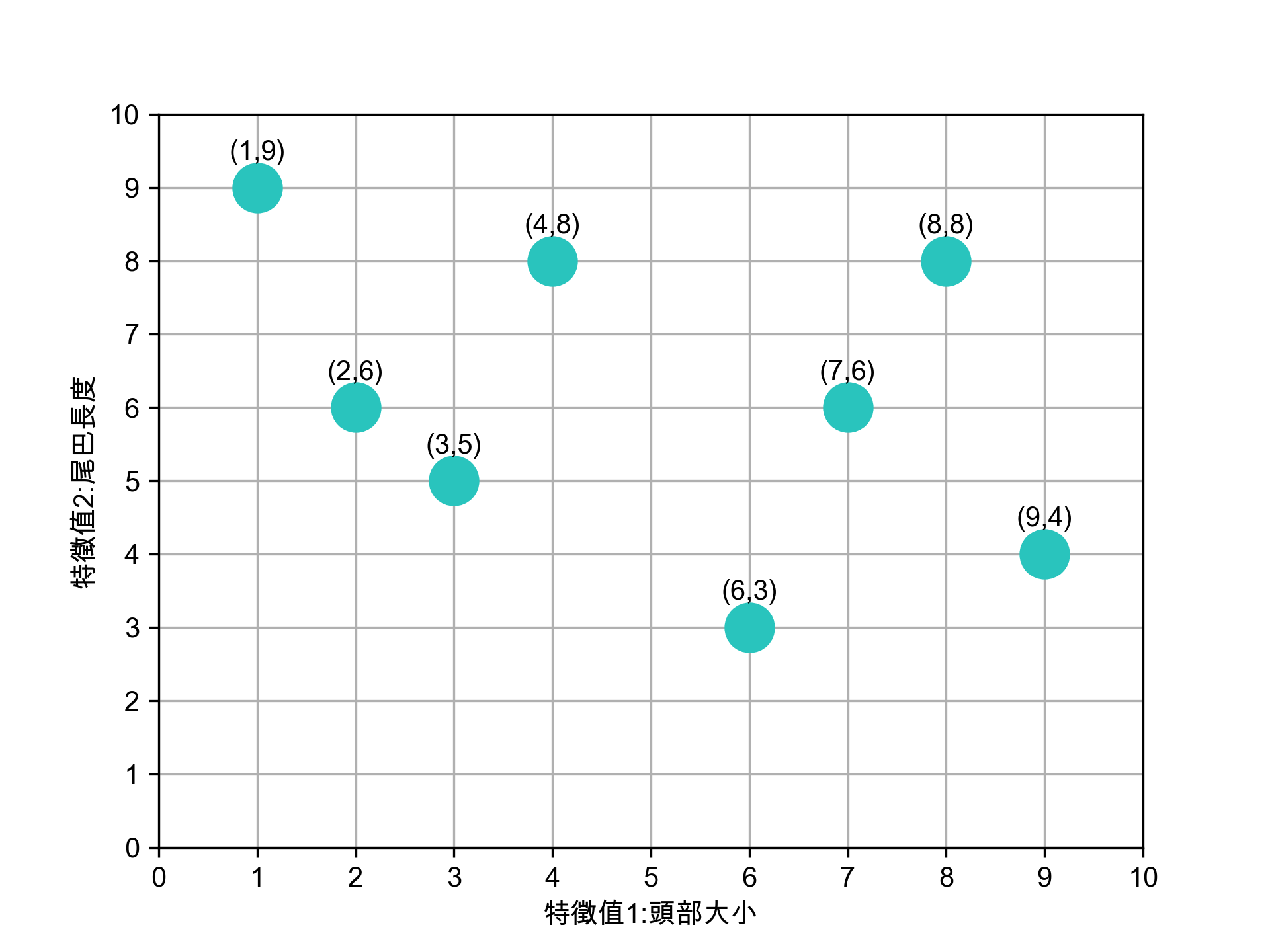
Figure 6: 待處理資料
K-means 演算法執行步驟如下:
2.1.1. 決定K值
K 值指的是現有訓練資料(八張照片)要分成的群數,此處K值為2。
2.1.2. 選定K個中心點
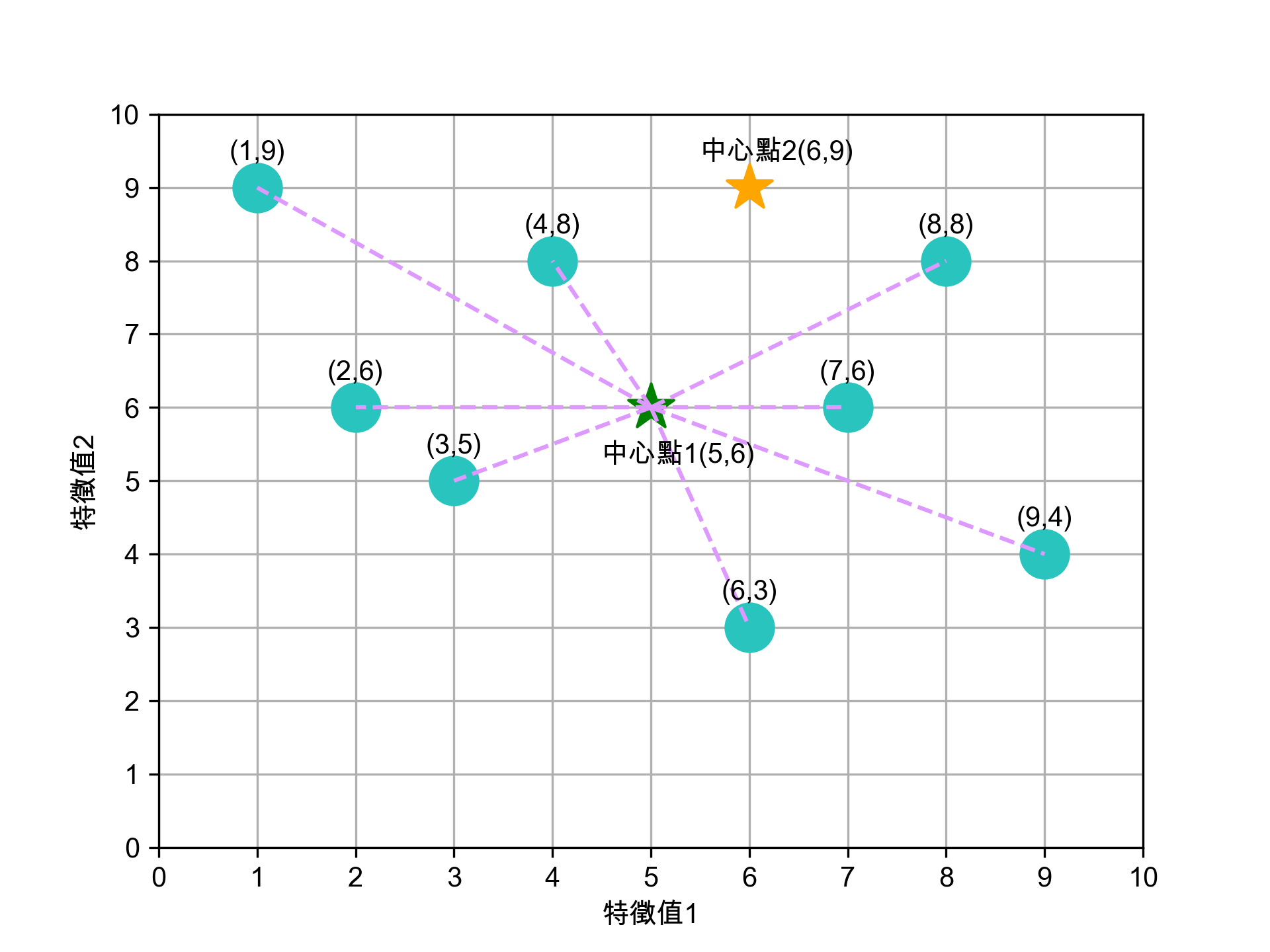
任意選定 K 個(K=2)中心點,在實際的程式實作可以亂數隨機產生這K個資料點。如圖7所示,隨機指定的兩群資料點的中心點為(5,5)、(6,9)。
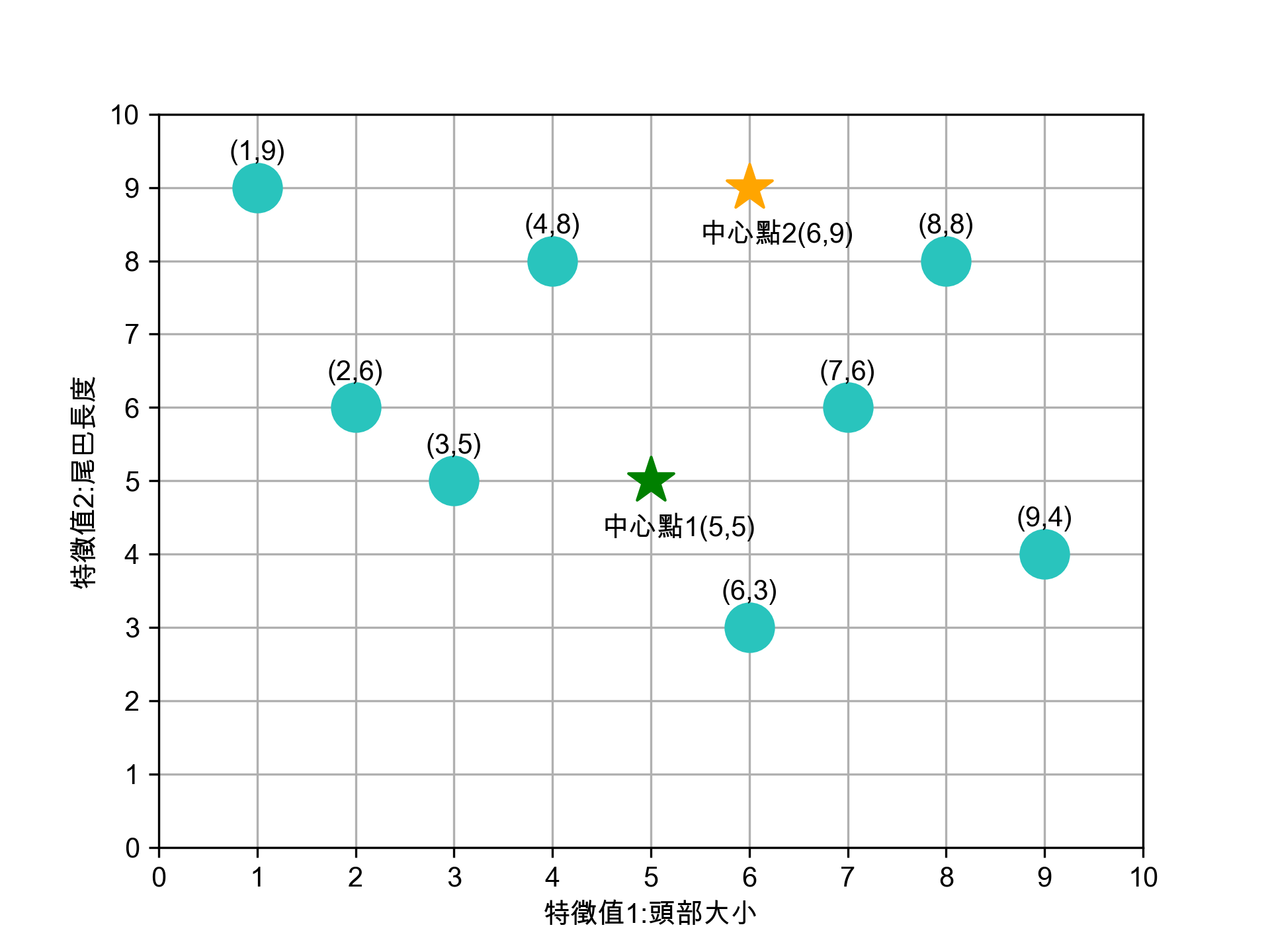
Figure 7: 標題
2.1.3. 將資料點分群
2.1.4. 為 K 個群裡的資料點找出新中心點
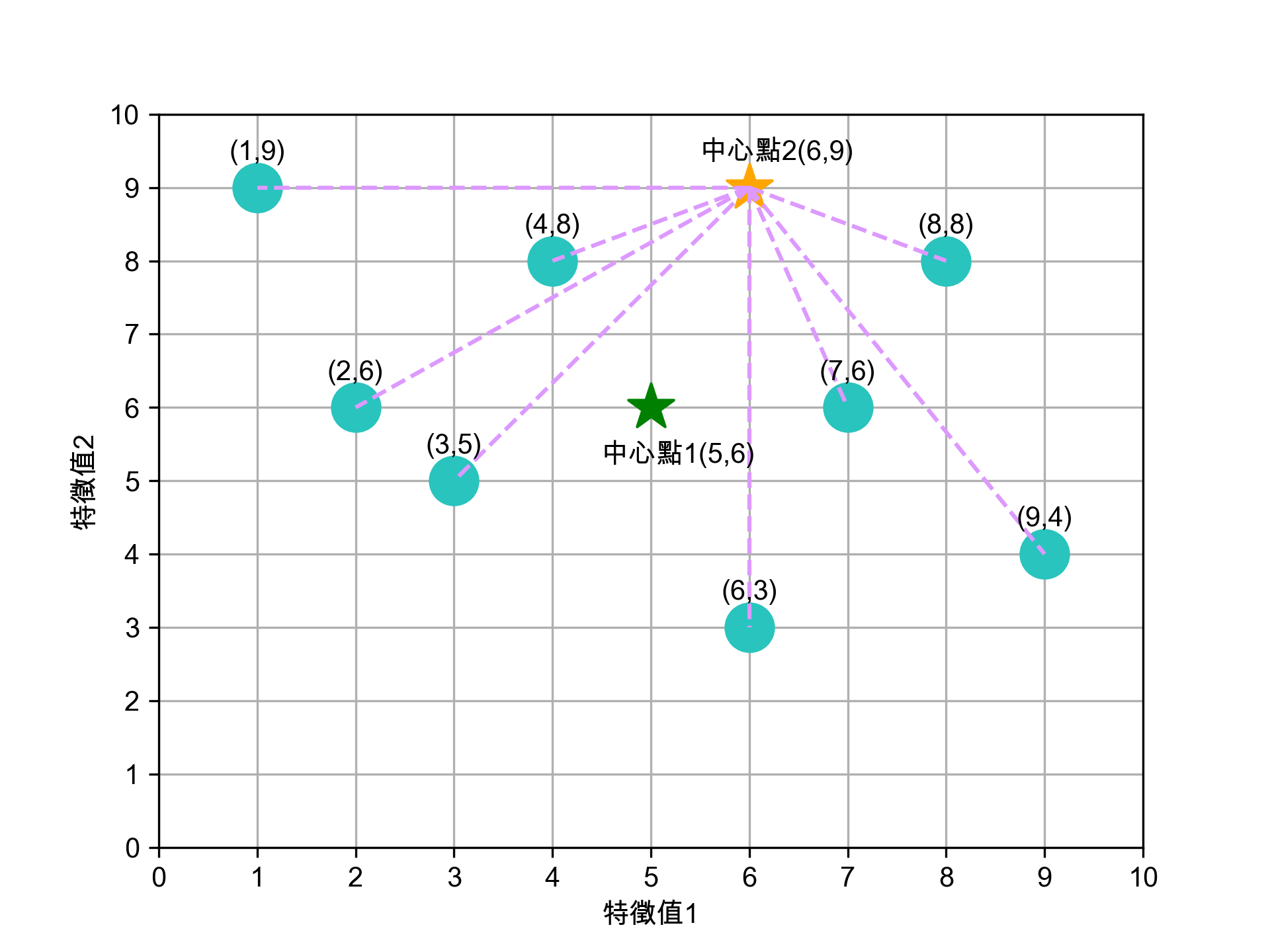
依前一步驟的分類,此 8 張資料點已分為兩群,接下來我們再為這兩群資料點找出各自的新中心點,計算方式如下:
- 新★X值: 2+3+4+6+7+9 =5.17
- 新★Y值: 6+5+8+3+6+4 =5.33
- 新★X值:1+8=4.50
- 新★Y值:9+8=8.50
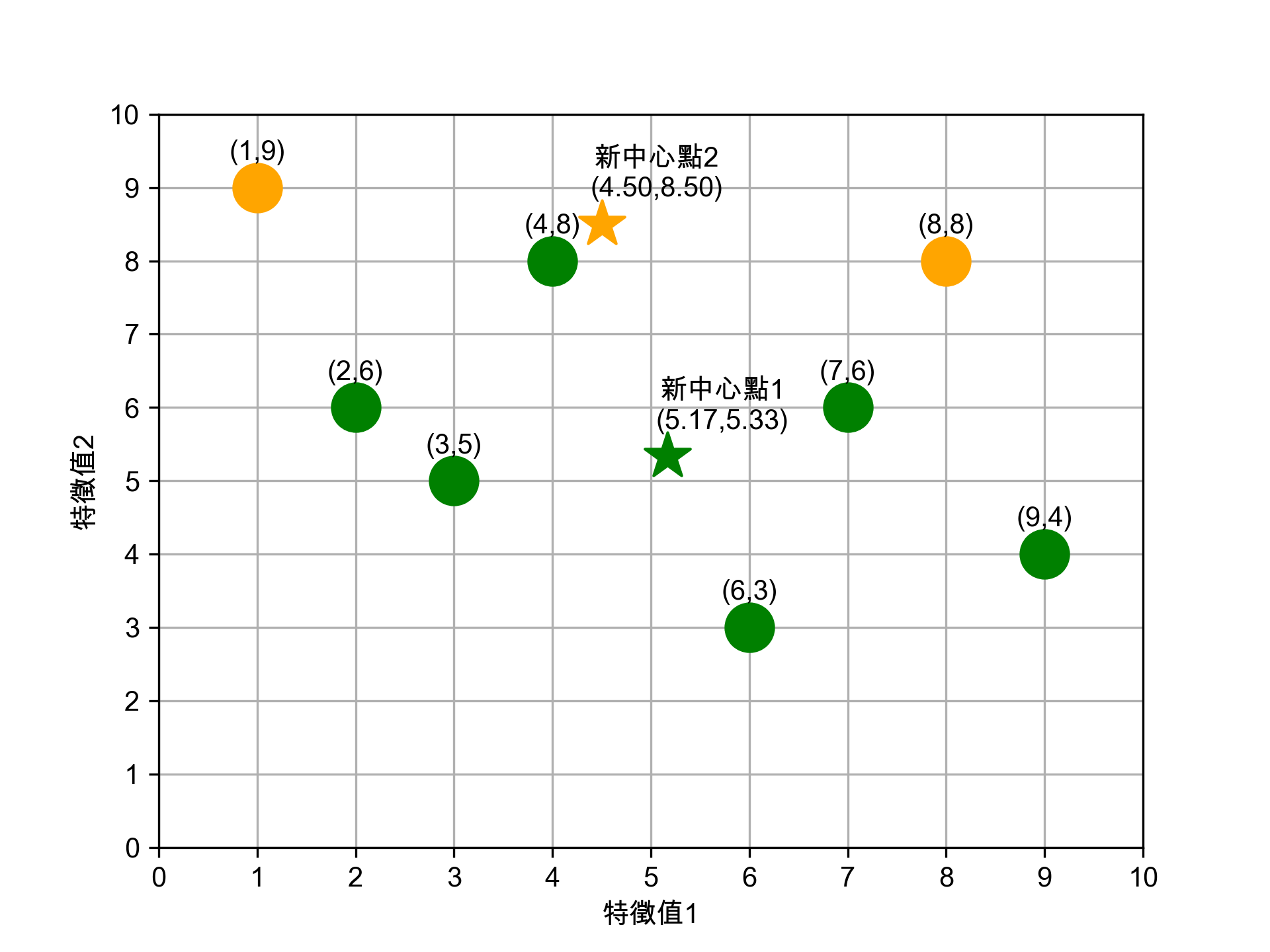
Figure 11: 標題
這個結果看起來不太合理對吧,至少(4,8)這點應該要歸入★這組才對。沒關係,因為還沒完成。
2.1.5. 重覆步驟 (3)、(4) 進行下一輪的分群,直到分群結果不再變化
接下來就繼續計算各點到新中心點★(5.17, 5.33)、★(4.50, 8.50)的距離、依新的距離重新對資料點進行分群(即步驟3),再求出新的中心點(即步驟4),如此重覆不斷進行,直到分群結果不再變動即告完成。
2.1.6. 如何訂K值
- 用K-means演算法需設定「K值」,但難免會面臨難以決定分群數量的狀況。同樣的資料如果要分成3群、4群、5群,就必須做三次不同的操作,而且分群的結果彼此之間不一定有其關聯性。
- 利用「階層式分群法」透過階層架構的方式,以對特徵距離的分析,將資料層層反覆地進行分裂或聚合,彈性決定群數。
2.2. K-Means實作:隨機數字 sklearn
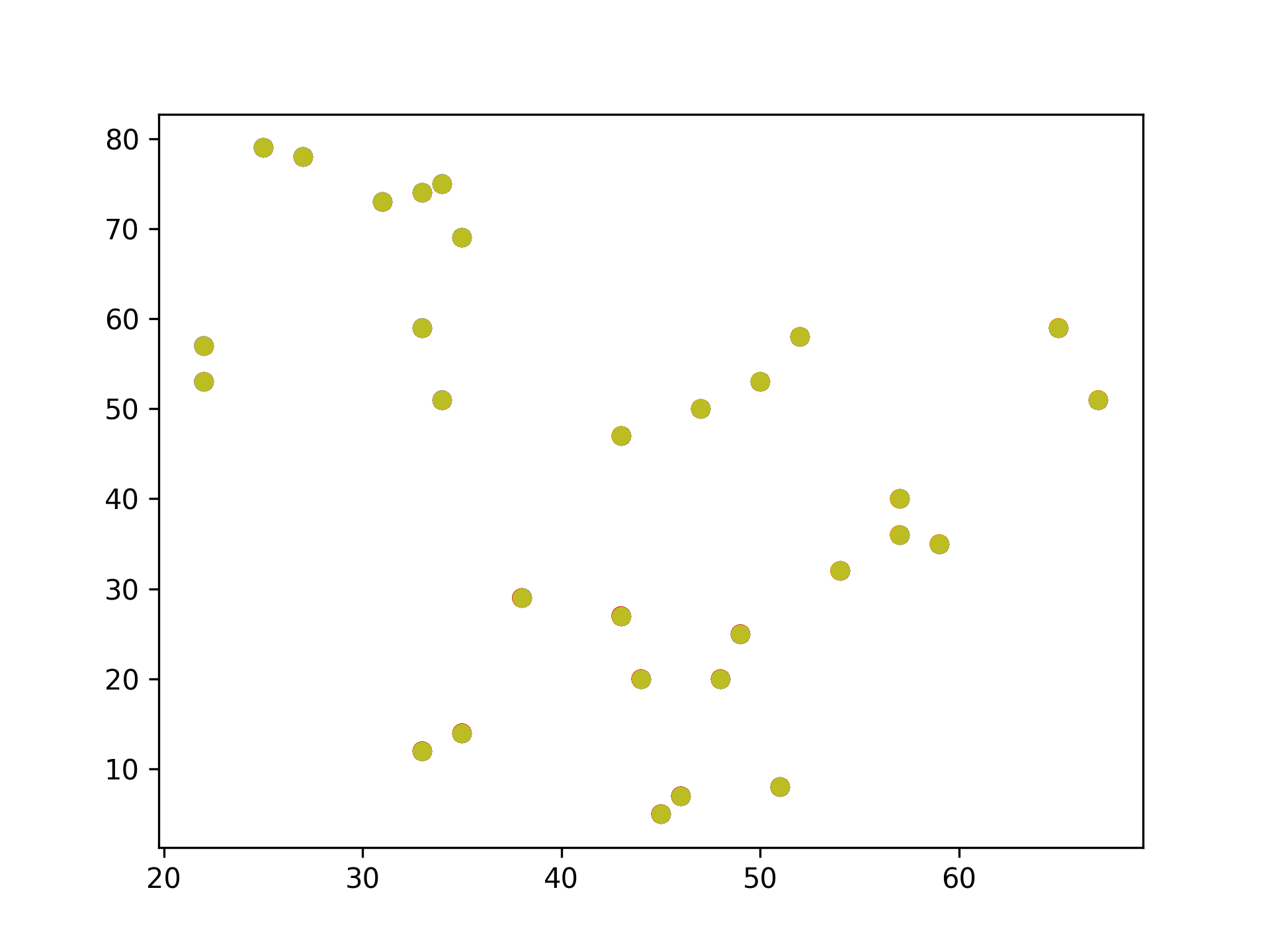
Figure 12: 原始資料
1: # 隨機生成100個(x, y) 2: import pandas as pd 3: data = { 4: 'x': [25, 34, 22, 27, 33, 33, 31, 22, 35, 34, 67, 54, 57, 43, 50, 57, 59, 52, 65, 47, 49, 48, 35, 33, 44, 45, 38, 5: 43, 51, 46], 6: 'y': [79, 51, 53, 78, 59, 74, 73, 57, 69, 75, 51, 32, 40, 47, 53, 36, 35, 58, 59, 50, 25, 20, 14, 12, 20, 5, 29, 27, 7: 8, 7] 8: } 9: samples = pd.DataFrame(data) 10: 11: import matplotlib.pyplot as plt 12: from sklearn.cluster import KMeans 13: 14: kmeans = KMeans(n_clusters=3) #預計分為三群,迭代次數由模型自行定義 15: kmeans.fit(samples) 16: cluster = kmeans.predict(samples) 17: 18: plt.scatter(samples['x'], samples['y'], c=cluster, cmap=plt.cm.Set1) 19: plt.savefig("images/kmeansScatter.png", dpi=300) 20: #plt.show()
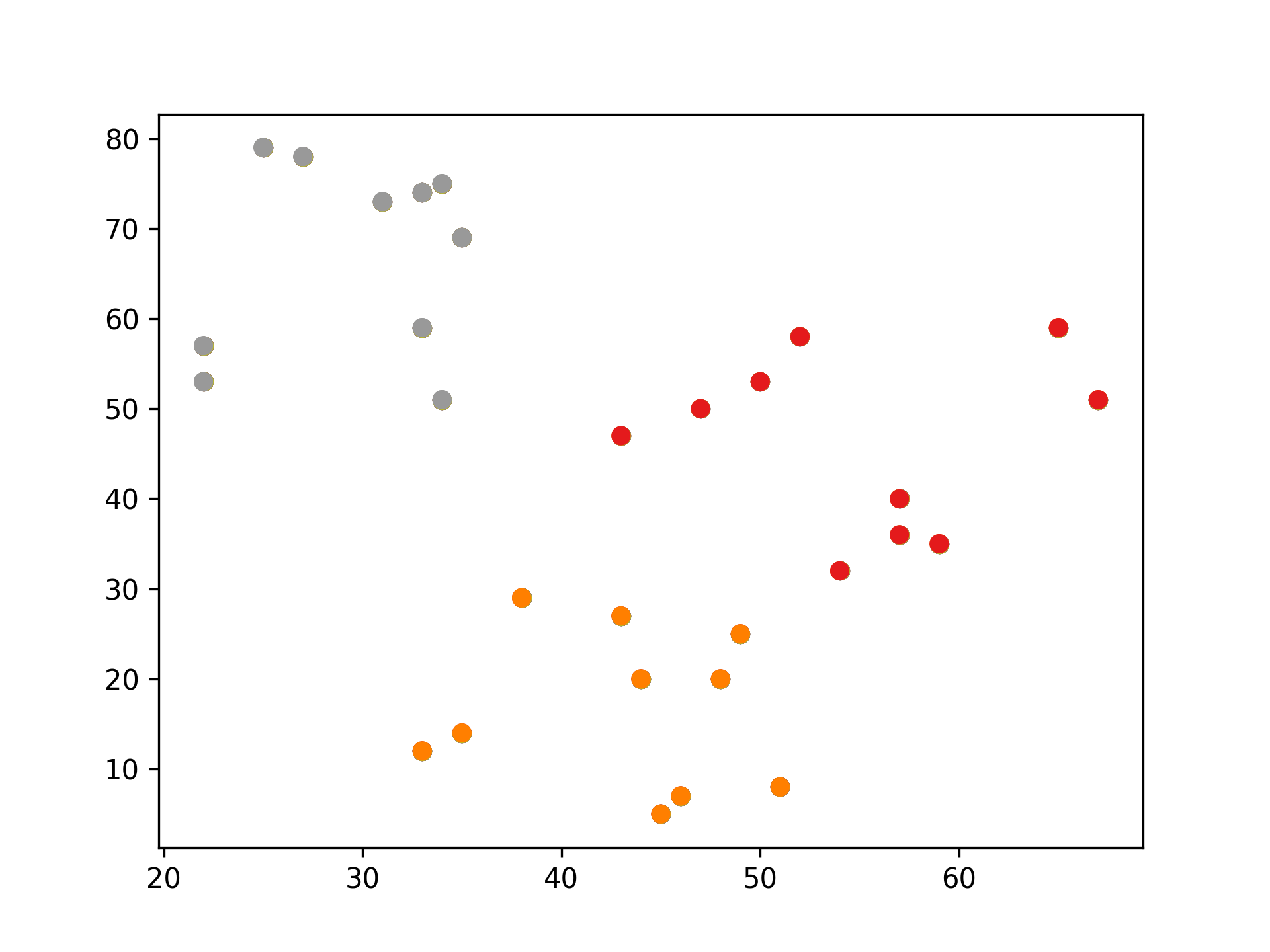
Figure 13: scikit-KMeans
2.3. K-Means應用: 壓縮影像
1: import numpy as np 2: import matplotlib.pyplot as plt # 需安裝 pillow 才能讀 JPEG 3: from matplotlib import image 4: from sklearn.cluster import MiniBatchKMeans 5: 6: # K 值 (要保留的顏色數量) 7: K = 4 8: # 讀取圖片 9: image = image.imread(r'./images/Photo42.jpg') 10: w, h, d = tuple(image.shape) 11: image_data = np.reshape(image, (w * h, d))/ 255 12: # 將顏色分類為 K 種 13: kmeans = MiniBatchKMeans(n_clusters=K, batch_size=10) 14: labels = kmeans.fit_predict(image_data) 15: centers = kmeans.cluster_centers_ 16: # 根據分類將顏色寫入新的影像陣列 17: image_compressed = np.zeros(image.shape) 18: label_idx = 0 19: for i in range(w): 20: for j in range(h): 21: image_compressed[i][j] = centers[labels[label_idx]] 22: label_idx += 1 23: 24: plt.imsave(r'images/compressTest.jpg', image_compressed)

Figure 14: 以KMeans壓縮圖片色彩
2.4. [小組作業]K-Means分群實作 TNFSH
以K-Means對鳶尾花資料(特徵值)進行分群
作業內容須包含:
- 程式碼
- 以不同特徵值(\(C^4_2\))配對進行cluster,畫出scatter
- 以不同特徵值(\(C^4_3\))配對進行cluster,畫出3D scatter
- 對於輸出之結果應輔以文字說明解釋。
- 以pdf繳交報告,報告首頁需列出組員列表(姓名、教學網ID)
2.5. [小組作業]以K-Means壓縮影像實作 TNFSH
參考前述[K-Means應用: 壓縮影像],自行找一張圖(jpg)進行以下測試
- 以不同K值、batchSize進行影像壓縮,並探討在不同情況下的壓縮效果(包含影像大小及品質)
- 以不同類型(顏色數量:全彩、256色、灰階)的圖片進行測試
- 對於輸出之結果應輔以文字說明解釋。
- 以pdf繳交報告,報告首頁需列出組員列表(姓名、教學網ID)
3. Hierarchical clustering
階層式分群法(Hierarchical Clustering)透過一種階層架構的方式,將資料層層反覆地進行分裂或聚合,以產生最後的樹狀結構,常見的方式有兩種:
聚合式階層分群法(Agglomerative Clustering): 是一種“bottom-up”的方法,也就是先準備好解決問題可能所需的基本元件或方案,再將這些基本元件組合起來,由小而大最後得到整體。因此在階層式分群法中,就是將每個資料點都視為一個個體,再一一聚合1,如圖152。
/2024-02-11_21-29-19_2024-02-11_21-28-47.png)
Figure 15: Buttom-up
分裂式階層分群法(Divisive Clustering): 是一種“top-down”的方法,先對問題有整體的概念,然後再逐步加上細節,最後讓整體的輪廓越來越清楚。而此法在階層式分群法中,先將整個資料集視為一體,再一一的分裂1,如圖162。
/2024-02-11_21-30-15_2024-02-11_21-30-06.png)
Figure 16: Top-down
3.1. 聚合式階層分群法(Agglomerative)
如果採用聚合的方式,階層式分群法可由樹狀結構的底部開始,將資料或群聚逐次合併。
聚合式階層分群步驟:
- 將各個資料點先視為個別的「群」。
- 比較各個群之間的距離,找出距離最短的兩個群。
- 將其合併變成一個新群。
- 不斷重複直到群的數量符合所要求的數目。
3.1.1. 聚合式階層分群: step by step
假設現在有6筆資料,分別標記A、B、C、D、E及F,且每筆資料都是一個群。
/2024-02-11_09-04-56_2024-02-11_09-04-42.png)
Figure 17: hierar-1
首先找距離最近的兩個群,在此例為A、B。將A與B結合為新的一群G1,就將這些點分成五群了,其中有四群還是單獨的點。
/2024-02-11_09-06-09_2024-02-11_09-06-00.png)
Figure 18: 標題
接著,再繼續找距離最近的兩個群,依此範例應為D與E,結合為新的一群G2。
/2024-02-11_09-06-59_2024-02-11_09-06-54.png)
Figure 19: 標題
將F與G2合而為新的群G3,這時,這些資料已經被分為三群了。
/2024-02-11_09-18-01_2024-02-11_09-07-48.png)
Figure 20: 標題
3.1.2. 如何定義兩個群聚之間的距離
單一連結聚合
Single-linkage agglomerative algorithm, 群聚與群聚間的距離可以定義為不同群聚中最接近兩點間的距離。
在分屬不同的兩群中,選擇最接近的兩點之距離,即代表兩群間的距離。因此在群與群間進行聚合時,依據此值最小者做為選取下一步結合之對象。
/2024-02-11_10-13-45_2024-02-11_09-23-14.png)
Figure 21: 標題
公式: \( d(G1, G2)=\min\limits_{ A \in G1, B \in G2 } d(A,B)\)
G1、G3與C之間如何聚合?
- G1與C之間的距離d(G1,C)=d(B,C)
- G3與C之間的距離d(G3,C)=d(F,C)
- G1與G3之間的距離d(G1,G3)=d(B,D)
計算完各群間的距離後,可知d(G3,C)為最短距離,因此G3將與C聚合,成為新群G4。
/2024-02-11_10-16-41_2024-02-11_10-16-28.png)
Figure 22: 標題
倘若要再聚合,由於剩下G1與G4,可聚合成為G5。
/2024-02-11_10-17-37_2024-02-11_10-17-28.png)
Figure 23: 標題
完整連結聚合
Complete-linkage agglomerative algorithm, 群聚間的距離定義為不同群聚中最遠兩點間的距離,這樣可以保證這兩個集合合併後, 任何一對的距離不會大於 d。
在分屬不同的兩群中,選擇最遠的兩點之距離,即代表兩群間的距離。因此在群與群間進行聚合時,依據此值最小者做為選取下一步結合之對象。
公式: \(d(G1,G2)=\max\limits_{A \in G1, B \in G2}d(A,B)\)
/2024-02-11_10-18-31_2024-02-11_10-18-24.png)
Figure 24: 標題
G1、G3與C之間如何聚合?
- G1與C之間的距離d(G1,C)=d(A,C)
- G3與C之間的距離d(G3,C)=d(E,C)
- G1與G3之間的距離d(G1,G3)=d(A,E)
/2024-02-11_10-20-11_2024-02-11_10-20-03.png)
Figure 25: 標題
計算完各群間的距離後,可知d(G1,C)為最短距離,因此G1將與C聚合,成為新群G4。
倘若要再聚合,由於剩下G3與G4,可聚合成為G5。
/2024-02-11_10-21-08_2024-02-11_10-21-02.png)
Figure 26: 標題
平均連結聚合
Average-linkage agglomerative algorithm, 群聚間的距離定義為不同群聚間各點與各點間距離總和的平均。沃德法(Ward’s method):群聚間的距離定義為在將兩群合併後,各點到合併後的群中心的距離平方和。
在分屬不同的兩群中,各點之距離的平均,即代表兩群間的距離。因此在群與群間進行聚合時,依據此值最小者做為選取下一步結合之對象。 G1、G3與C之間如何聚合?
/2024-02-11_10-24-58_2024-02-11_10-24-49.png)
Figure 27: 標題
公式: \(d(G1,G2)=\sum\limits_{A \in G1, B \in G2}\frac{d(A,B)}{|G1|\times|G2|}\)
- \( d(G1, C)=\frac{d(A,C)+d(B,C)}{2\times1}\)
- \( d(G3, C)=\frac{d(D,C)+d(E,C)+d(F,C)}{3\times1}\)
- \( d(G1, G3)=\frac{d(A,D)+d(A,E)+d(A,F)+d(B,D)+d(B,E)+d(B,F)}{2\times3}\)
3.1.3. 決定群數
可以依照使用者的群數需求或相似度要求,來決定要在哪一層時停止聚合資料。若以完整連結的群間距離計算方式為例,圖上的虛線代表不同的群數,端看使用者需求來決定。
/2024-02-11_10-47-21_2024-02-11_10-47-15.png)
Figure 28: 標題
3.1.4. 聚合式階層分群實作
scikit-learn: Agglomerative Clustering
- 分兩群
1: from sklearn.cluster import AgglomerativeClustering 2: import matplotlib.pyplot as plt 3: import numpy as np 4: 5: # randomly chosen dataset 6: X = np.array([[1, 2], [1, 4], [1, 0], [2, 1], [2, 3], [2, 4], 7: [3, 1], [3, 3], [3, 4], [4, 2], [4, 4], [4, 0]]) 8: clustering = AgglomerativeClustering(n_clusters = 2).fit(X) 9: print('分兩群:',clustering.labels_)
分兩群: [0 1 0 0 1 1 0 1 1 0 1 0]
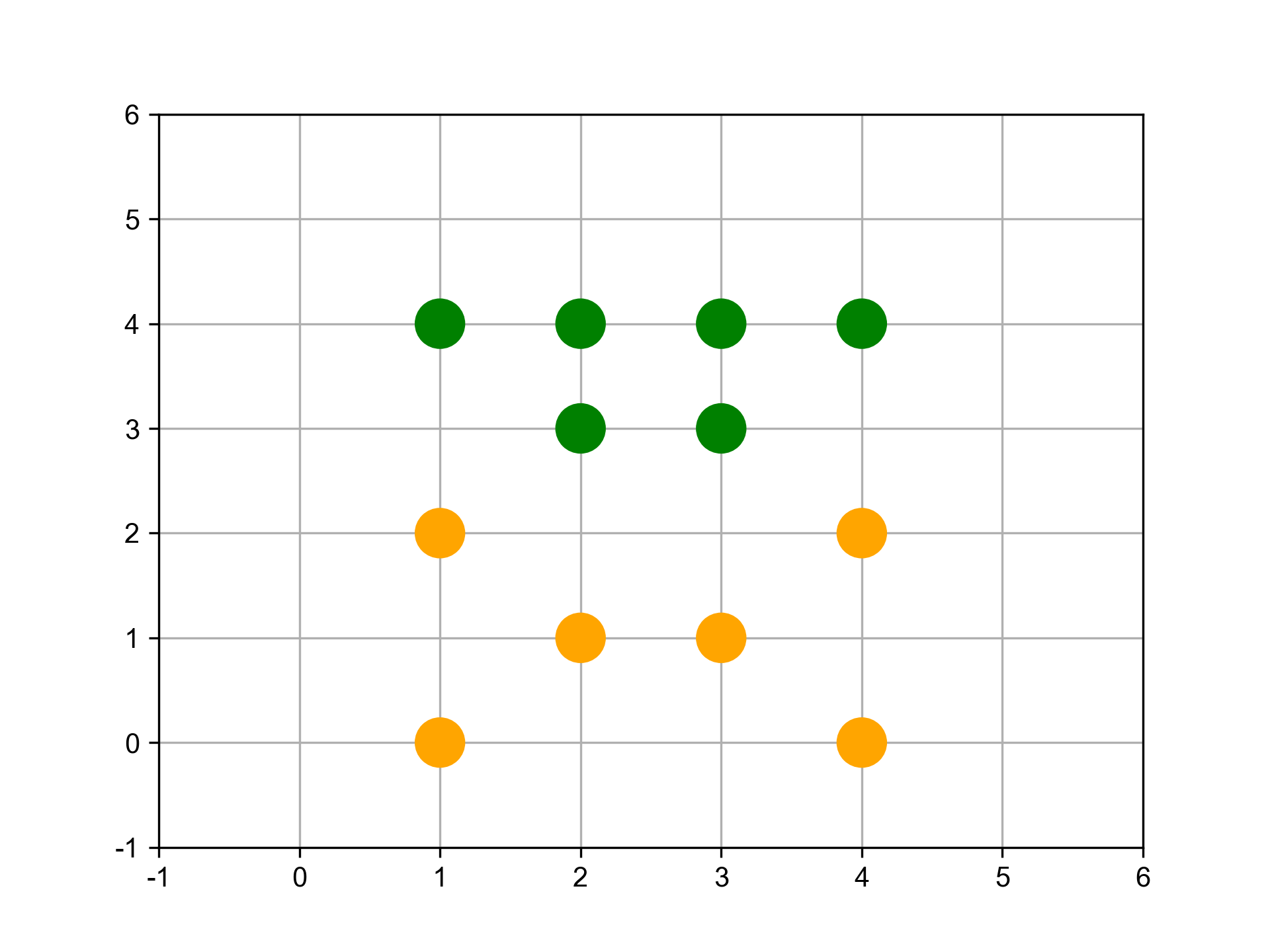
Figure 29: 分成兩組
- 分三群
1: clustering = AgglomerativeClustering(n_clusters = 3).fit(X) 2: print('分三群:',clustering.labels_)
分三群: [1 0 1 1 0 0 1 0 0 2 0 2]
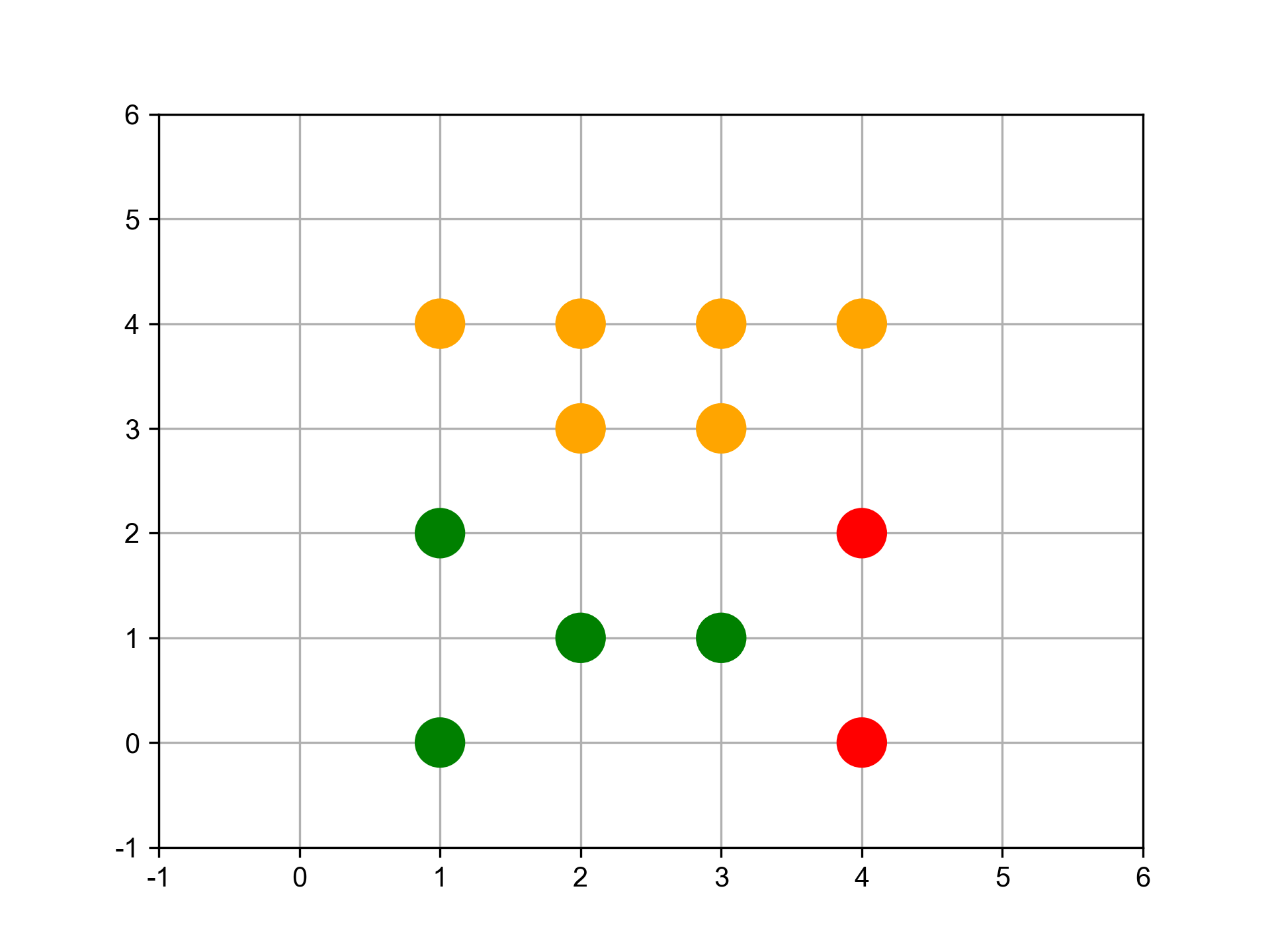
Figure 30: 分成三群
- 分四群
1: clustering = AgglomerativeClustering(n_clusters = 4).fit(X) 2: print('分四群:',clustering.labels_)
分四群: [0 3 0 0 3 3 0 1 1 2 1 2]
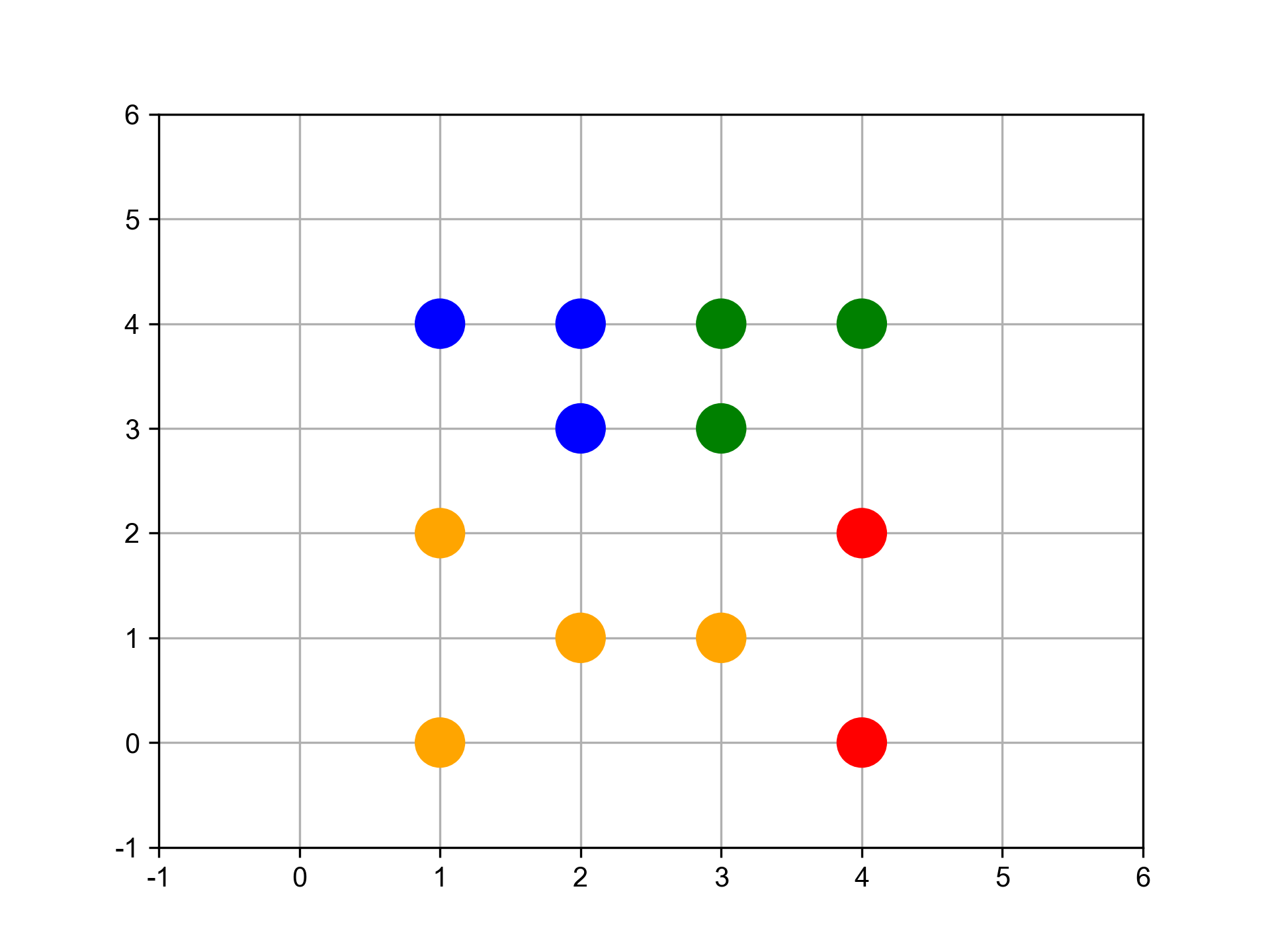
Figure 31: 分成四群
SciPy: scipy.cluster.hierarchy[一次分完]
1: import numpy as np 2: import matplotlib.pyplot as plt 3: import scipy.cluster.hierarchy as sch 4: 5: # randomly chosen dataset 6: X = np.array([[1, 2], [1, 4], [1, 0], [2, 1], [2, 3], [2, 4], 7: [3, 1], [3, 3], [3, 4], [4, 2], [4, 4], [4, 0]]) 8: y = np.array(['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L']) 9: 10: dis=sch.linkage(X,metric='euclidean', method='ward') 11: #metric: 距離的計算方式 12: #method: 群與群之間的計算方式,”single”, “complete”, “average”, 13: # “weighted”, “centroid”, “median”, “ward” 14: 15: sch.dendrogram(dis, labels = y) 16: 17: plt.title('Hierarchical Clustering') 18: plt.xticks(rotation=30) 19: plt.savefig("images/hierarCluster-1.png", dpi=300) 20: #plt.show()
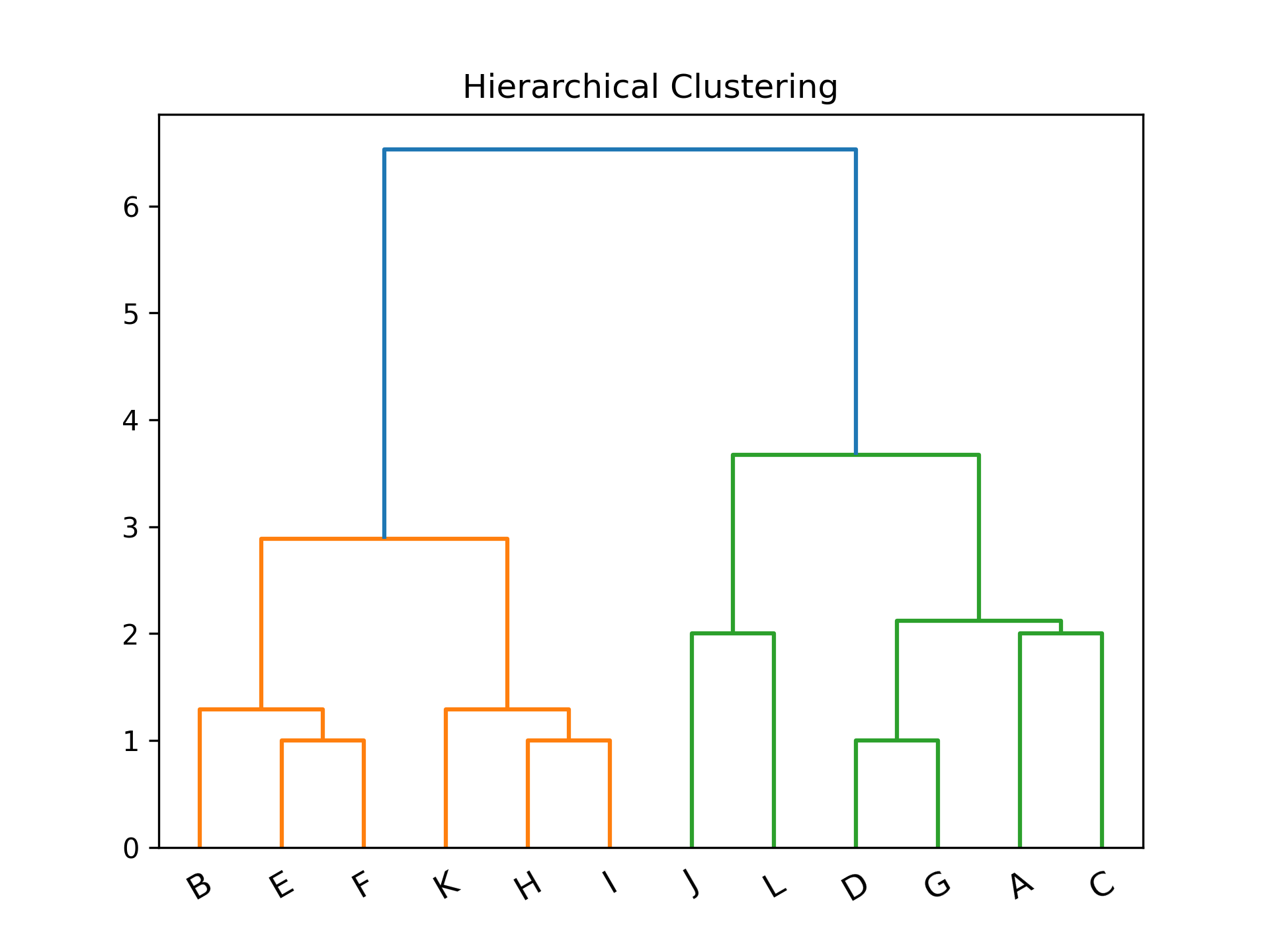
Figure 32: Hierarchical Clustering
SciPy: scipy.cluster.hierarchy[逐步分群]
1: import numpy as np 2: import matplotlib.pyplot as plt 3: import scipy.cluster.hierarchy as sch 4: 5: # randomly chosen dataset 6: X = np.array([[1, 2], [1, 4], [1, 0], [2, 1], [2, 3], [2, 4], 7: [3, 1], [3, 3], [3, 4], [4, 2], [4, 4], [4, 0]]) 8: y = np.array(['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L']) 9: 10: #metric: 距離的計算方式 11: #method: 群與群之間的計算方式,”single”, “complete”, “average”, “weighted”, “centroid”, “median”, “ward” 12: 13: plt.cla() 14: # Setting the truncate_mode to 'lastp' to see incremental clustering 15: plt.figure(figsize=(10, 20)) 16: for i in range(2, len(y) + 1): 17: plt.subplot( 6, 2, i - 1) 18: labels = y[:i] # Adjusting labels for each step 19: x_step = X[:i] 20: dis=sch.linkage(x_step, metric='euclidean', method='ward') 21: sch.dendrogram(dis, labels=labels, truncate_mode='lastp', p=i) 22: plt.title(f'Step {i}') 23: 24: plt.suptitle('Hierarchical Clustering Steps') 25: plt.tight_layout(rect=[0, 0.03, 1, 0.95]) 26: 27: plt.title('Hierarchical Clustering') 28: plt.xticks(rotation=30) 29: plt.savefig("images/hierarCluster-2.png", dpi=300) 30: #plt.show()
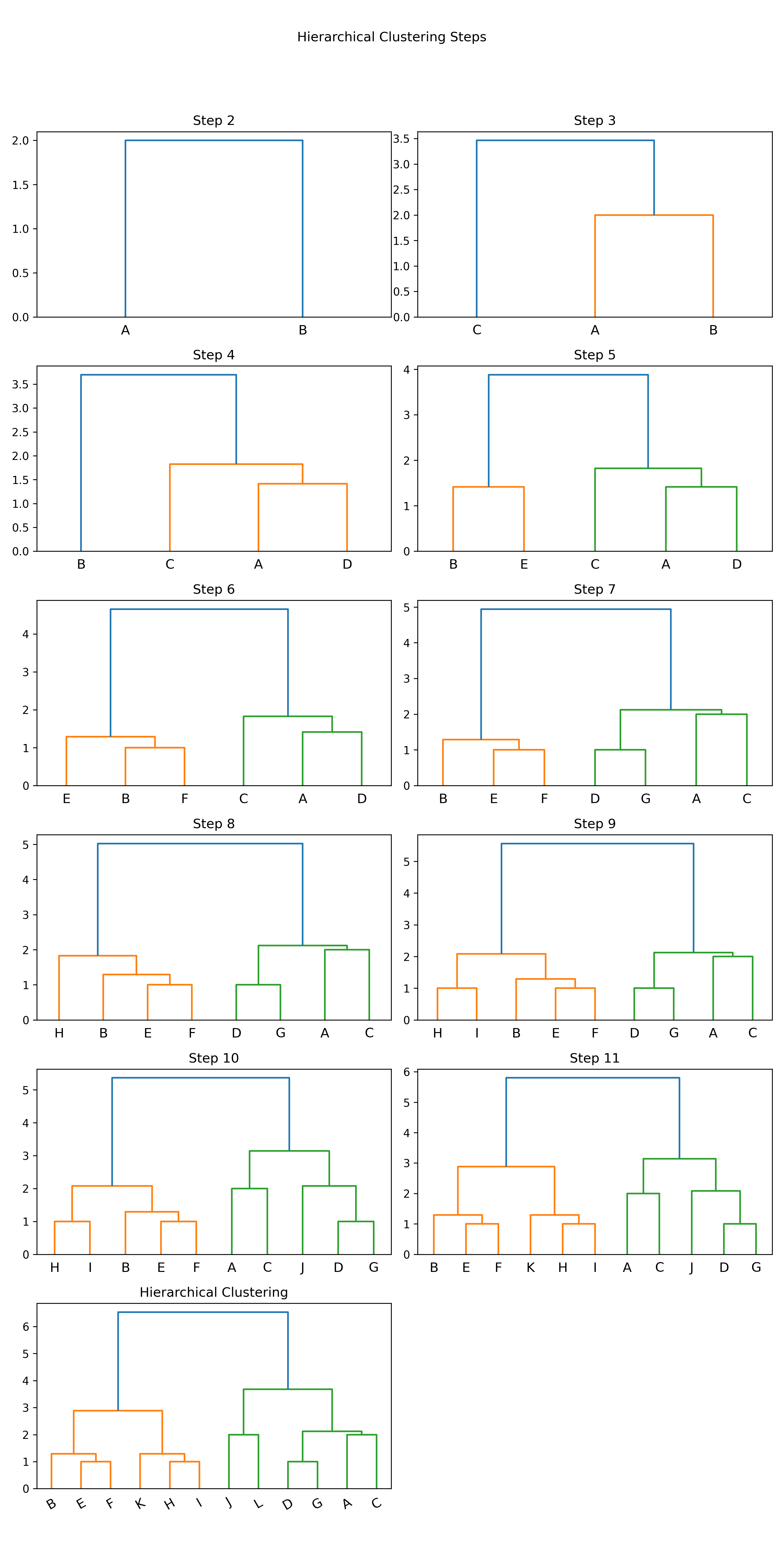
Figure 33: Hierarchical Clustering
利用距離決定群數,或直接給定群數
建構好聚落樹狀圖後,我們可以依照距離的切割來進行分類,也可以直接給定想要分類的群數,讓系統自動切割到相對應的距離。
- 距離切割 所給出的樹狀圖,y軸代表距離,我們可以用特徵之間的距離進行分群的切割。
1: max_dis=5 2: clusters=sch.fcluster(dis,max_dis,criterion='distance') 3: import matplotlib.pyplot as plt 4: plt.figure() 5: plt.scatter(X[:,0], X[:,1], c=clusters, cmap=plt.cm.Set1) 6: plt.savefig("images/clusterScatter.png", dpi=300)
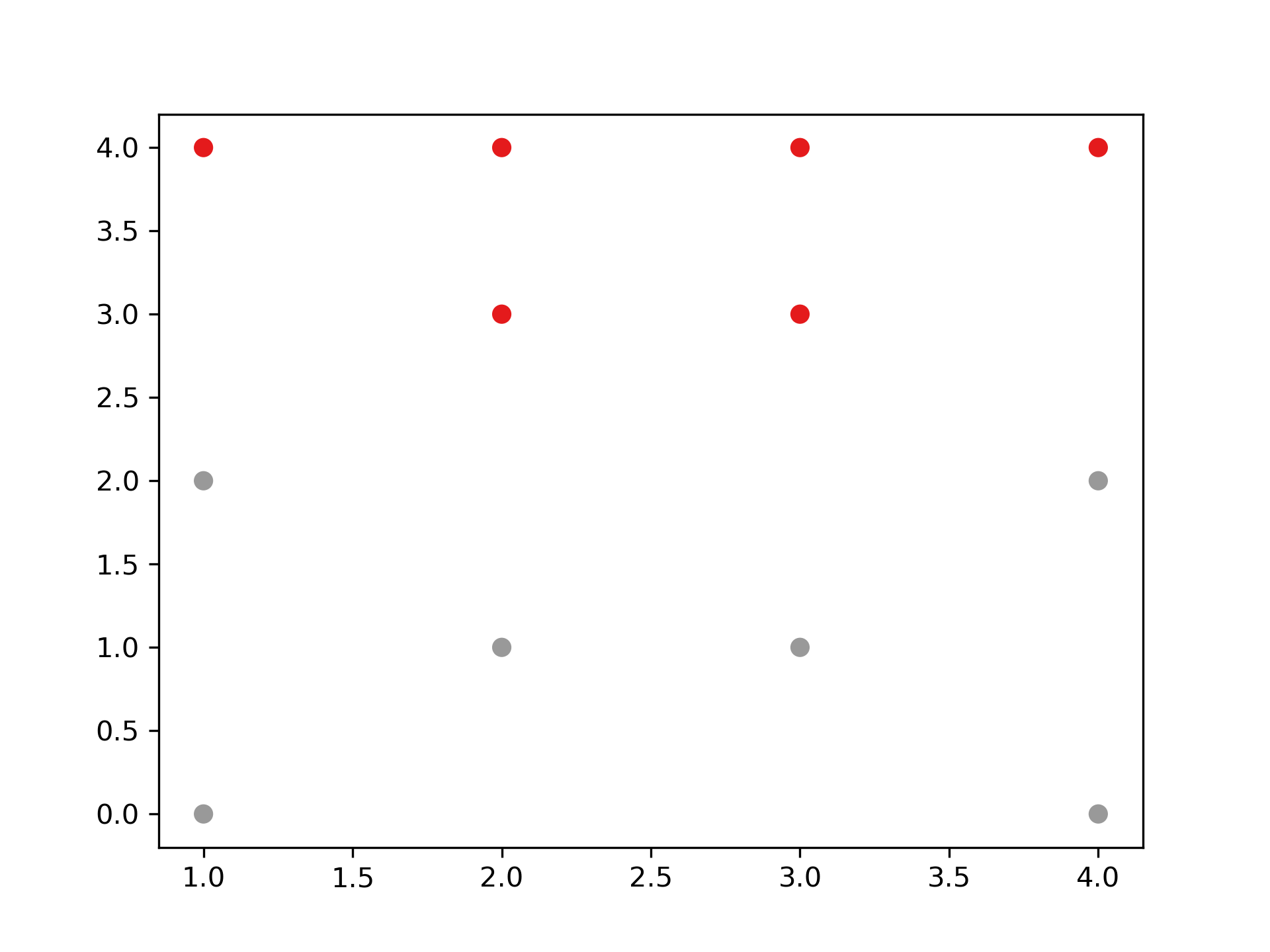
Figure 34: Caption
- 直接給定群數 同時,我們也可以像sklearn一樣,直接給定我們所想要分出的群數。
1: k=4 2: clusters=sch.fcluster(dis,k,criterion='maxclust') 3: 4: import matplotlib.pyplot as plt 5: plt.figure() 6: plt.scatter(X[:,0], X[:,1], c=clusters, cmap=plt.cm.Set1) 7: plt.savefig("images/clusterScatter-1.png", dpi=300)
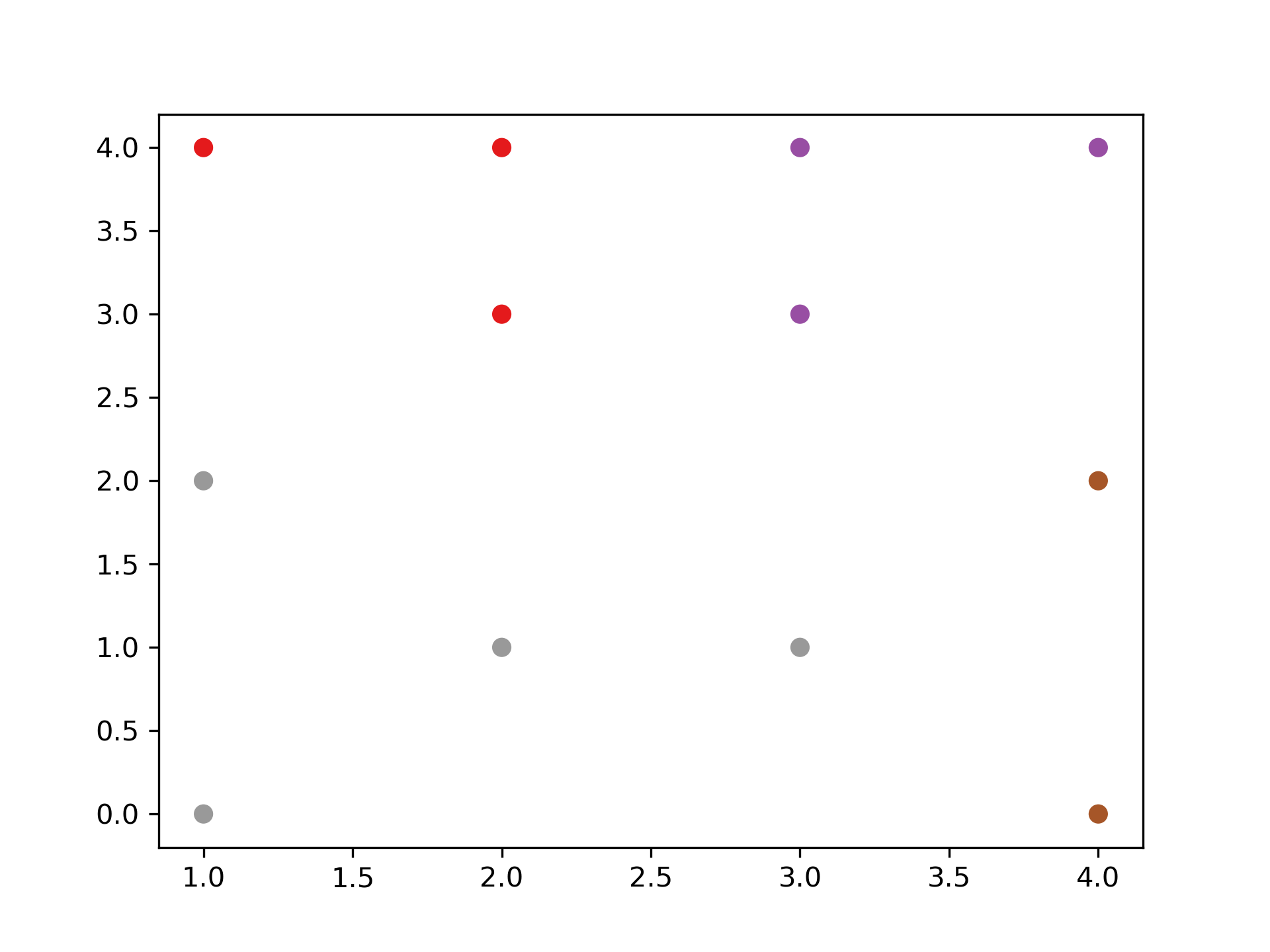
Figure 35: Caption
3.1.5. 如何評估最佳分群數:K
3.2. [課堂任務]聚合式階層分群 TNFSH
3.2.1. 資料
在此給定資料並以數值化座標平面表示,其中包含A、B、C、D、E、F、G及H共8個點。假設B與C點合併為G1;G與H點合併為G2,而G2加入F點後形成G3。 每個資料點有兩個特徵值(如圖36):
- x = np.array([1,2,3,2,5,5,6,7])
- y = np.array([4,2,2,6,5,0,1,2])
/2024-02-14_15-43-38_2024-02-14_15-43-04.png)
Figure 36: 資料分佈圖
3.2.2. 任務1
請利用「單一連結」的群間距離計算方式完成聚合式階層式分群。
/2024-02-14_15-45-04_2024-02-14_15-44-51.png)
Step 1
/2024-02-14_16-05-52_2024-02-14_16-05-35.png)
| A | D | E | G1 | G3 | |
|---|---|---|---|---|---|
| A | |||||
| D | |||||
| E | |||||
| G1 | |||||
| G3 |
註: A可與D或與G1合併,在此選擇將A與G1合併為G4。
Step 2
/2024-02-14_15-51-00_2024-02-14_15-50-44.png)
| D | E | G3 | G4 | |
|---|---|---|---|---|
| D | ||||
| E | ||||
| G3 | ||||
| G4 |
Step 3
/2024-02-14_15-53-20_2024-02-14_15-53-08.png)
| E | G3 | G5 | |
|---|---|---|---|
| E | |||
| G3 | |||
| G5 |
Step 4
/2024-02-14_15-54-50_2024-02-14_15-54-36.png)
| E | G6 | |
|---|---|---|
| E | ||
| G6 |
3.2.3. 任務2
請利用「完整連結」的群間距離計算方式完成聚合式階層式分群。
/2024-02-14_15-45-04_2024-02-14_15-44-51.png)
Step 1
/2024-02-14_16-09-10_2024-02-14_16-09-01.png)
| A | D | E | G1 | G3 | |
|---|---|---|---|---|---|
| A | |||||
| D | |||||
| E | |||||
| G1 | |||||
| G3 |
Step 2
/2024-02-14_16-14-30_2024-02-14_16-14-22.png)
| E | G1 | G3 | G4 | |
|---|---|---|---|---|
| E | ||||
| G1 | ||||
| G3 | ||||
| G4 |
註: G4可與E或與G1合併,在此選擇將G4與G1合併為G5。
Step 3
/2024-02-14_16-15-28_2024-02-14_16-15-15.png)
| E | G3 | G5 | |
|---|---|---|---|
| E | |||
| G3 | |||
| G5 |
Step 4
/2024-02-14_16-16-33_2024-02-14_16-16-28.png)
| G3 | G6 | |
|---|---|---|
| G3 | ||
| G6 |
3.2.4. 任務3
請利用「平均連結」的群間距離計算方式完成聚合式階層式分群。
/2024-02-14_15-45-04_2024-02-14_15-44-51.png)
Step 1
/2024-02-14_16-18-48_2024-02-14_16-18-39.png)
| A | D | E | G1 | G3 | |
|---|---|---|---|---|---|
| A | |||||
| D | |||||
| E | |||||
| G1 | |||||
| G3 |
Step 2
/2024-02-14_16-22-19_2024-02-14_16-22-13.png)
| E | G1 | G3 | G4 | |
|---|---|---|---|---|
| E | ||||
| G1 | ||||
| G3 | ||||
| G4 |
Step 3
/2024-02-14_16-24-31_2024-02-14_16-24-25.png)
| E | G3 | G5 | |
|---|---|---|---|
| E | |||
| G3 | |||
| G5 |
Step 4
/2024-02-14_16-25-47_2024-02-14_16-25-40.png)
| G3 | G6 | |
|---|---|---|
| G3 | ||
| G6 |
3.2.5. 任務4
請以「單一連結」完成之聚合式階層式分群結果,寫出各種不同分群數量時,各群所包含的資料內容。
/2024-02-14_16-29-58_2024-02-14_16-29-33.png)
3.3. TNFSH作業: 聚合式分群作業 TNFSH
電子商務網站黃色鬼屋近日收集了200位VIP客戶資料,想將這些客戶依其同質性進行分類。
3.3.1. 資料
/2024-02-14_15-28-32_2024-02-14_15-28-25.png)
Figure 37: 黃色鬼屋VIP資料
- 資料集URL: https://raw.githubusercontent.com/letranger/AI/gh-pages/Downloads/schopaholic.csv
- CID: 客戶編號
- Gd: 性別(Male/Female)
- Age: 年齡
- Income: 月收入(單位為萬元)
- ShopSco: 這是黃色鬼屋自訂的敗家分數,範圍由0~100
3.3.2. 任務
畫出200位VIP客戶的性別、年齡、月收入、敗家分數的分佈狀況,例如:
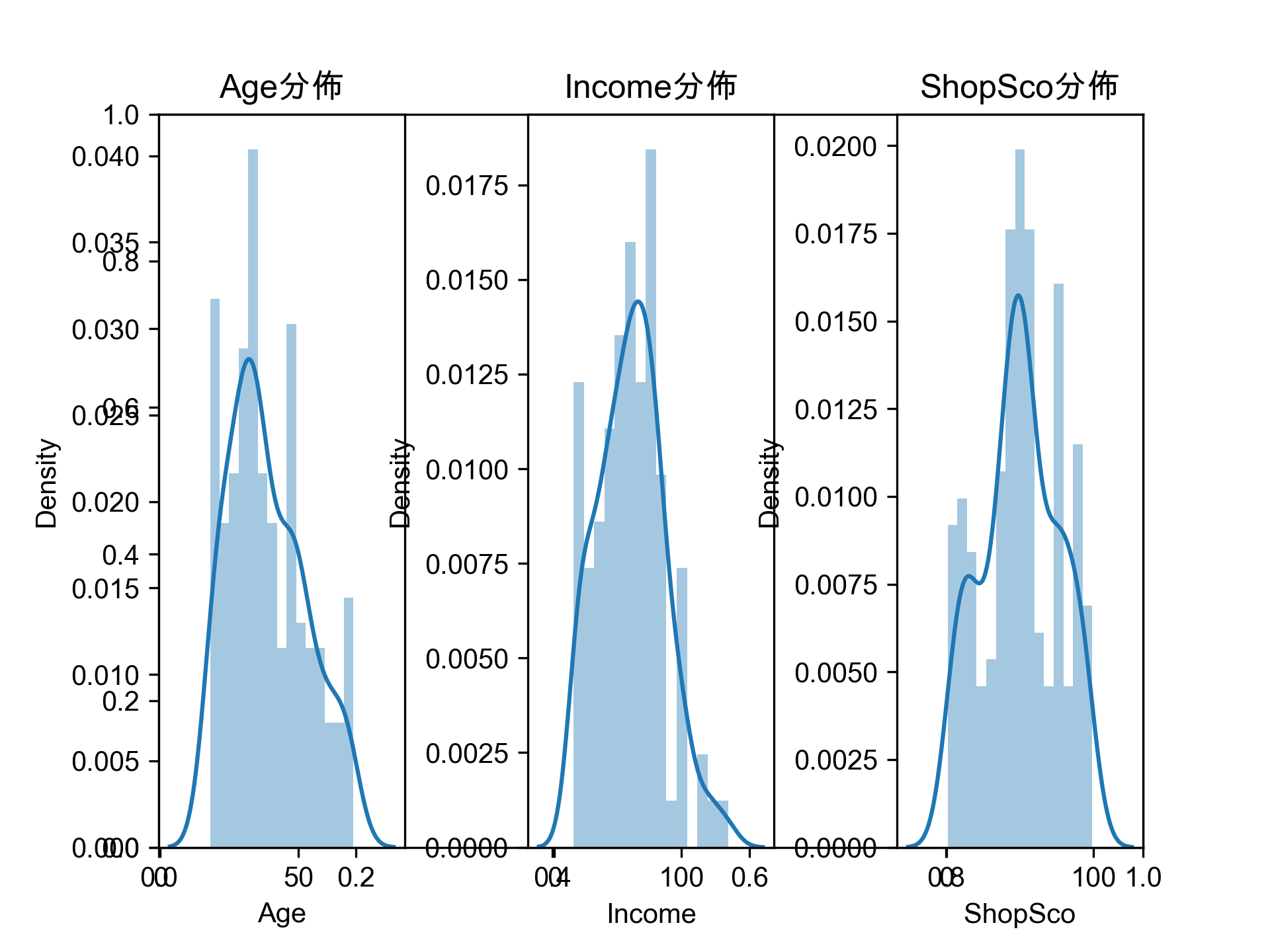
- 利用聚合式分群的模型幫黃色鬼屋完成以下工作
將階層圖畫出來,例如:
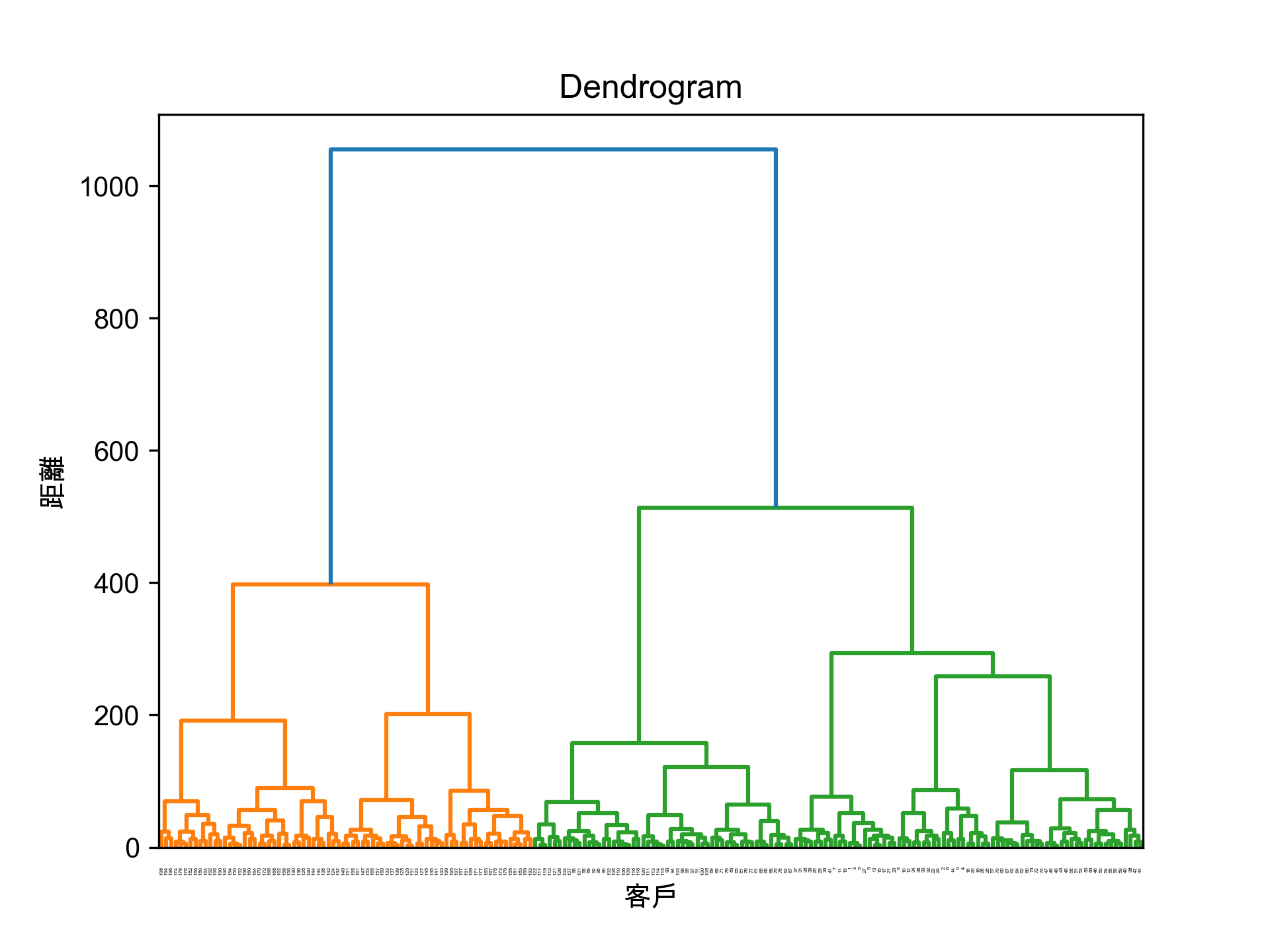
輸出分成5群的結果,例如:
第1群客戶ID: 127 129 131 135 ... 第2群客戶ID: 28 44 46 47 48 ... 第3群客戶ID: 124 126 128 130 ... 第4群客戶ID: 2 4 6 8 10 12 14 ... 第5群客戶ID: 1 3 5 7 9 11 13 ...
3.4. 分裂式階層分群法(Divisive Clustering)
如果採用分裂的方式,則由樹狀結構的頂端開始,將群聚逐次分裂。步驟:
- 將所有資料先視為同一群,再依據群內的相異,分裂成兩群。
- 接著,再從兩群中,找群內相異度最高的那群,再分裂一次,變成三群…,重複操作直到分出來的群數達到目標群數。
3.4.1. 分裂式階層分群實作
Figure 38: Caption
4. DBSCAN
DBSCAN(密度式分群)會將「彼此靠得很近」的點群組在一起,其中「靠近」是指在某個指定距離範圍內,必須存在最少數量的點。如果一個點同時位於多個群的距離範圍內,則它會被歸類到其中密度最高的群。任何不在任何群的距離範圍內的點,則會被標記為離群值(outlier)。
在 K-means 和階層式分群中,所有資料點都必須被分到某個群內,這使得離群值常被處理得很差。而 DBSCAN 則可以明確地標記離群值,避免必須強行將它們納入群中,這是一項很強大的特性。與其他分群演算法相比,DBSCAN 對資料中的離群值不容易受到扭曲影響。
此外,像階層式分群一樣 —— 不同於 K-means —— DBSCAN 不需要事先指定群的數量。
4.1. 實作
4.1.1. 讀入資料
1: '''Main''' 2: import numpy as np 3: import pandas as pd 4: import os, time, pickle, gzip 5: import datetime 6: 7: '''Data Prep''' 8: from sklearn import preprocessing as pp 9: 10: '''Data Viz''' 11: import matplotlib.pyplot as plt 12: import matplotlib as mpl 13: import seaborn as sns 14: color = sns.color_palette() 15: # Load the datasets 16: current_path = os.getcwd() 17: file = os.path.sep.join(['', 'datasets', 'mnist.pkl.gz']) 18: 19: f = gzip.open(current_path+file, 'rb') 20: train_set, validation_set, test_set = pickle.load(f, encoding='latin1') 21: f.close() 22: 23: X_train, y_train = train_set[0], train_set[1] 24: X_validation, y_validation = validation_set[0], validation_set[1] 25: X_test, y_test = test_set[0], test_set[1] 26: 27: # Create Pandas DataFrames from the datasets 28: train_index = range(0,len(X_train)) 29: validation_index = range(len(X_train), len(X_train)+len(X_validation)) 30: test_index = range(len(X_train)+len(X_validation), \ 31: len(X_train)+len(X_validation)+len(X_test)) 32: 33: X_train = pd.DataFrame(data=X_train,index=train_index) 34: y_train = pd.Series(data=y_train,index=train_index) 35: 36: X_validation = pd.DataFrame(data=X_validation,index=validation_index) 37: y_validation = pd.Series(data=y_validation,index=validation_index) 38: 39: X_test = pd.DataFrame(data=X_test,index=test_index) 40: y_test = pd.Series(data=y_test,index=test_index) 41:
4.1.2. 降維
1: # Principal Component Analysis 2: from sklearn.decomposition import PCA 3: 4: n_components = 784 5: whiten = False 6: random_state = 2018 7: 8: pca = PCA(n_components=n_components, whiten=whiten, \ 9: random_state=random_state) 10: 11: X_train_PCA = pca.fit_transform(X_train) 12: X_train_PCA = pd.DataFrame(data=X_train_PCA, index=train_index) 13: 14: # Log data 15: cwd = os.getcwd() 16: log_dir = cwd+"/datasets/" 17: y_train[0:2000].to_csv(log_dir+'labels.tsv', sep = '\t', index=False, header=False) 18: 19: # Write dimensions to CSV 20: X_train_PCA.iloc[0:2000,0:3].to_csv(log_dir+'pca_data.tsv', sep = '\t', index=False, header=False)
4.1.3. DBSCAN
1: # Perform DBSCAN 2: def analyzeCluster(clusterDF, labelsDF): 3: countByCluster = pd.DataFrame(data=clusterDF['cluster'].value_counts()) 4: countByCluster.reset_index(inplace=True,drop=False) 5: countByCluster.columns = ['cluster','clusterCount'] 6: 7: preds = pd.concat([labelsDF,clusterDF], axis=1) 8: preds.columns = ['trueLabel','cluster'] 9: 10: countByLabel = pd.DataFrame(data=preds.groupby('trueLabel').count()) 11: 12: countMostFreq = \ 13: pd.DataFrame(data=preds.groupby('cluster').agg( \ 14: lambda x:x.value_counts().iloc[0])) 15: countMostFreq.reset_index(inplace=True,drop=False) 16: countMostFreq.columns = ['cluster','countMostFrequent'] 17: 18: accuracyDF = countMostFreq.merge(countByCluster, \ 19: left_on="cluster",right_on="cluster") 20: overallAccuracy = accuracyDF.countMostFrequent.sum()/ \ 21: accuracyDF.clusterCount.sum() 22: 23: accuracyByLabel = accuracyDF.countMostFrequent/ \ 24: accuracyDF.clusterCount 25: 26: return countByCluster, countByLabel, countMostFreq, \ 27: accuracyDF, overallAccuracy, accuracyByLabel 28: 29: from sklearn.cluster import DBSCAN 30: 31: eps = 3 32: min_samples = 5 33: leaf_size = 30 34: n_jobs = 4 35: 36: db = DBSCAN(eps=eps, min_samples=min_samples, leaf_size=leaf_size, 37: n_jobs=n_jobs) 38: 39: cutoff = 99 40: X_train_PCA_dbscanClustered = db.fit_predict(X_train_PCA.loc[:,0:cutoff]) 41: X_train_PCA_dbscanClustered = \ 42: pd.DataFrame(data=X_train_PCA_dbscanClustered, index=X_train.index, \ 43: columns=['cluster']) 44: 45: countByCluster_dbscan, countByLabel_dbscan, countMostFreq_dbscan, \ 46: accuracyDF_dbscan, overallAccuracy_dbscan, accuracyByLabel_dbscan \ 47: = analyzeCluster(X_train_PCA_dbscanClustered, y_train) 48: 49: overallAccuracy_dbscan 50: # Print overall accuracy 51: print("Overall accuracy from DBSCAN: ",overallAccuracy_dbscan) 52: 53: # Show cluster results 54: print("Cluster results for DBSCAN") 55: countByCluster_dbscan 56:
Overall accuracy from DBSCAN: 0.242 Cluster results for DBSCAN
5. 降維
進行非監督式學習時,為了加速計算,最好能「在不損失過多資訊的前提下簡化資料」,降維(dimensionality reduction)就是其中一種手段。例如,汽車的里程數與車齡就有合併的依據。
- 本例以Colab為執行平台,透過資料的圖形化分佈觀察不同降維的效果。
- 於Colab執行時可以先將例中的savefig()註解掉
降維的主要目的在於壓縮資料,有以下幾種做法:
5.1. 以主成份分析(PCA)對非監督式數據壓縮
「特徵選擇」需要原始的「特徵」;而「特徵提取」則是在於「轉換」數據,或是「投影」(project)數據到一個新的「特徵空間」,特徵提取不僅能改善儲存空間的使用或是提高學習演算法的計算效率,也可以有效地藉由降低「維數災難」來提高預測的正確性,特別是在處理非正規化模型時。
5.1.1. 主成分分析 1
「主成份分析」(principal component analysis, PCA)是一種非監督式線性變換技術」,經常應用於「特徵提取」與「降維」,其他應用包括「探索式數據分析」和「股票市場分析」中的雜訊消除、生物資訊學領域中的「基因數據分析」與「基因表現層分析」。
這邊先簡單說維度詛咒,預測/分類能力通常是隨著維度數(變數)增加而上生,但當模型樣本數沒有繼續增加的情況下,預測/分類能力增加到一定程度之後,預測/分類能力會隨著維度的繼續增加而減小3。
主成份分析的基本假設是希望資料可以在特徵空間找到一個投影軸(向量)投影後可以得到這組資料的最大變異量。以圖39為例,PCA 的目的在於找到一個向量可以投影(圖中紅色的線),讓投影後的資料變異量最大。
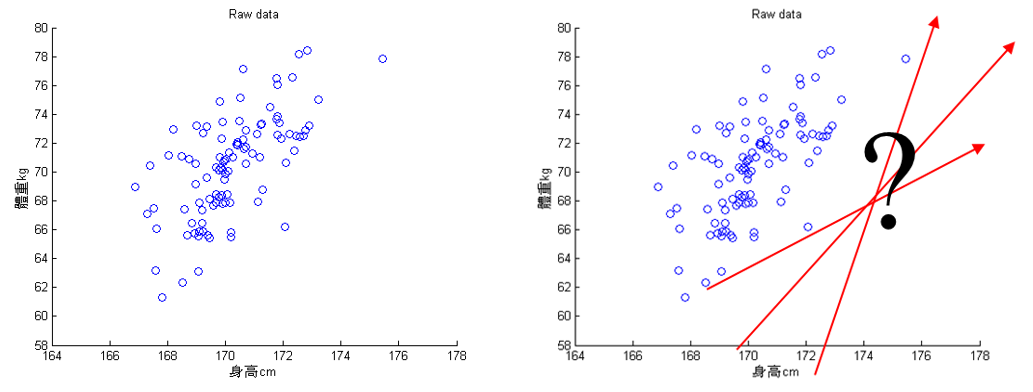
Figure 39: PCA-1 [fn:31]
投影(projection)
假設有一個點藍色的點對原點的向量為\(\vec{x_i}\),有一個軸為 v,他的投影(正交為虛線和藍色線為 90 度)向量為紅色那條線,紅色線和黑色線的夾角為\(\theta\),\(\vec{x_i}\)投影長度為藍色線,其長度公式為\(\left\|{x_i}\right\|cos\theta\)。
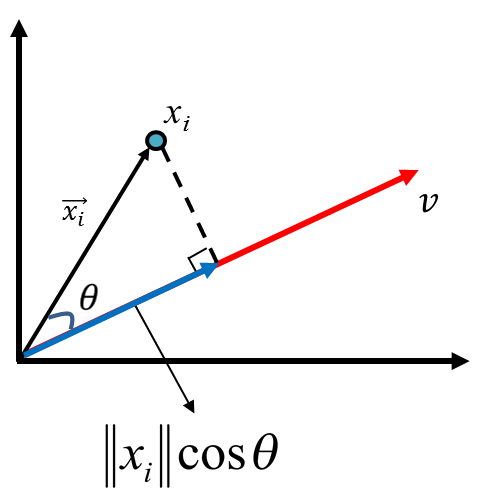
Figure 40: PCA-2 [fn:31]
假設有一組資料六個點(\(x_1, x_2, x_3, x_4, x_5, x_6\)),有兩個投影向量\(\vec{v}\)和\(\vec{v'}\)(如圖41),投影下來後,資料在\(\vec{v'}\)上的變異量比\(v\)上的變異量小。
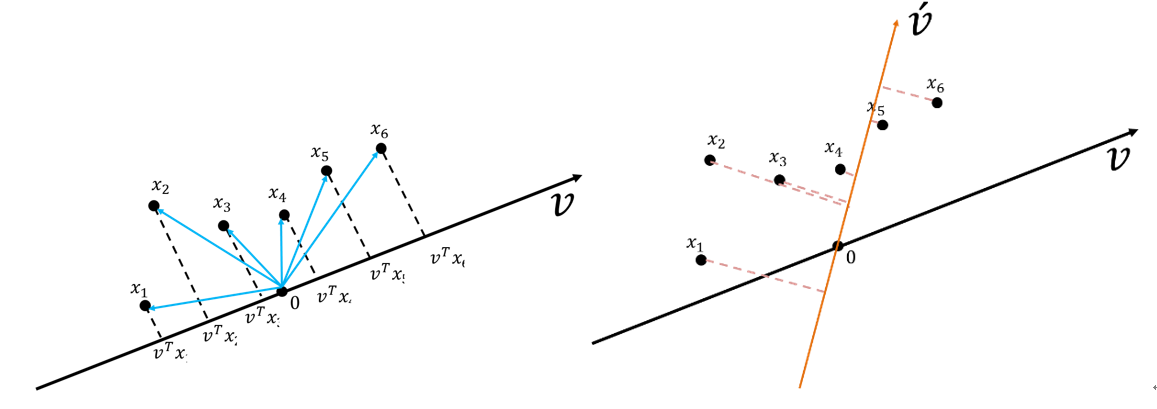
Figure 41: PCA-3 [fn:31]
從圖42也可以看出這些資料在\(v\)向量資料投影后有較大的變異量(較之投影於\(\vec{v'}\))。
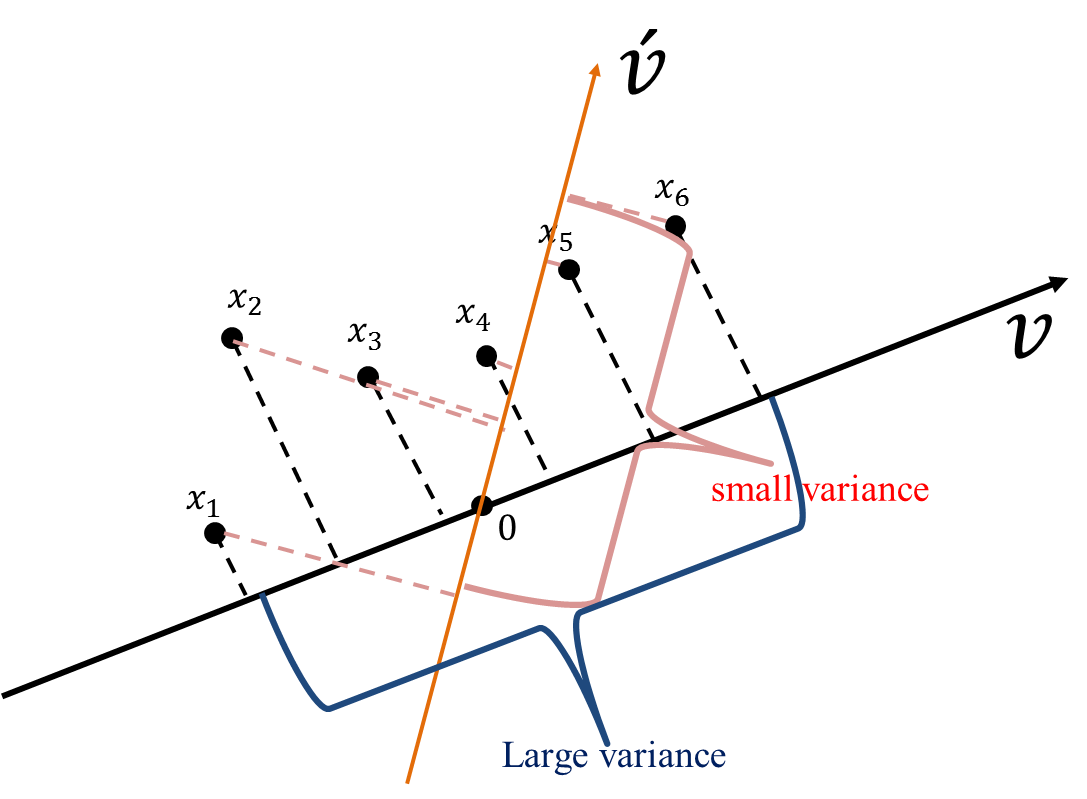
Figure 42: PCA-4 [fn:31]
變異量的計算
典型的變異數公式如下: \(\sigma^2 = \frac{1}{N}\sum\limits_{i=1}^N (X -\mu)^2\)
若要計算前述所有資料點(\(x_1, x_2, x_3, x_4, x_5, x_6\))在\(v\)上的投影\(v^Tx_1, v^Tx_2, v^Tx_3, v^Tx_4, v^Tx_5, v^Tx_6\) ,則其變異數公式為 \(\sigma^2 = \frac{1}{N}\sum\limits_{i=1}^N (v^Tx_i -\mu)^2\)
又因 PCA 之前提假設是將資 shift 到 0(即,變異數的平均數為 0)以簡化運算,其公式會變為 \(\sigma^2 = \frac{1}{N}\sum\limits_{i=1}^N (v^Tx_i -\mu)^2 = \frac{1}{N}\sum\limits_{i=1}^N (v^Tx_i - 0)^2 = \frac{1}{N}\sum\limits_{i=1}^N (v^Tx_i)^2\)
而機器學習處理的資料點通常為多變量,故上述式子會以矩陣方式呈現
\(\Sigma = \frac{1}{N}\sum\limits_{i=1}^N (v^Tx_i)(v^Tx_i)^T = \frac{1}{N}\sum\limits_{i=1}^N (v^Tx_iv^Tx_iv) = v^T(\frac{1}{N}\sum\limits_{i=1}^Nx_iX_i^T)v = v^TCv\)
其中 C 為共變異數矩陣(covariance matrix)
\(C=\frac{1}{n}\sum\limits_{i=1}^nx_ix_i^T,\cdots x_i = \begin{bmatrix} x_1^{(1)} \\ x_2^{(2)} \\ \vdots \\ x_i^{(d)} \\ \end{bmatrix}\)
主成份分析的目的則是在找出一個投影向量讓投影後的資料變異量最大化(最佳化問題):
\(v = \mathop{\arg\max}\limits_{x \in \mathcal{R}^d,\left\|v\right\|=1} {v^TCv}\)
進一步轉成 Lagrange、透過偏微分求解,其實就是解 C 的特徵值(eigenvalue, \(\lambda\))和特徵向量(eigenvector, \(v\))。
5.1.2. 主成份分析 2
回到前述例子(身高和體重),下左圖,經由 PCA 可以萃取出兩個特徵成分(投影軸,下圖右的兩條垂直的紅線,較長的紅線軸為變異量較大的主成份)。此範例算最大主成份的變異量為 13.26,第二大主成份的變異量為 1.23。
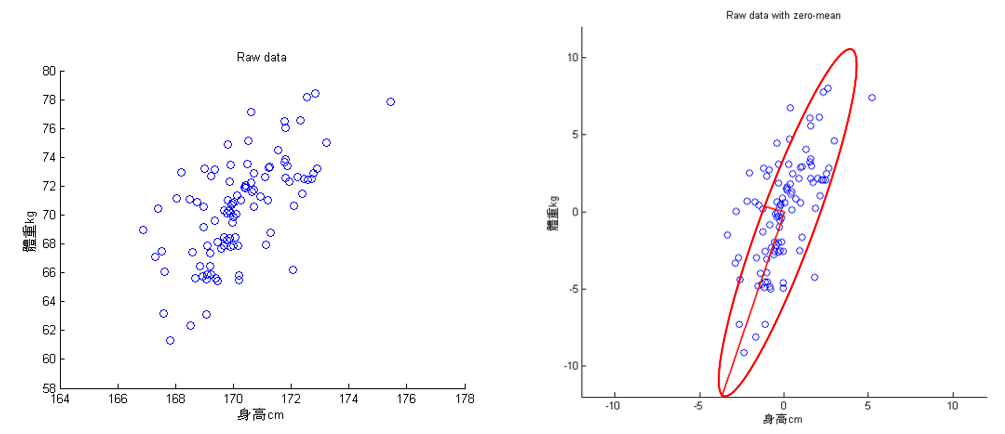
Figure 43: PCA-5 [fn:31]
PCA 投影完的資料為下圖,從下圖可知,PC1 的變異足以表示此筆資料資訊。
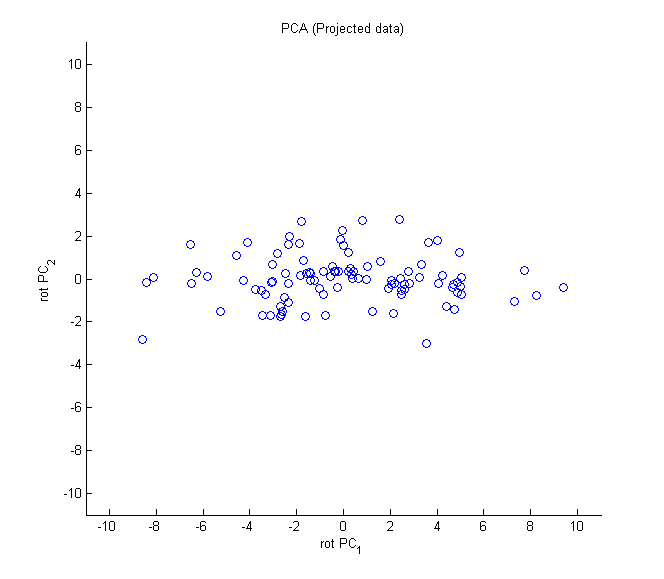
Figure 44: PCA-6 [fn:31]
此做法可以有效的減少維度數,但整體變異量並沒有減少太多,此例從兩個變成只有一個,但變異量卻可以保留(13.26/(13.26+1.23)= 91.51%),兩維度的資料做 PCA,對資料進行降維比較沒有感覺,但講解圖例比較容易。
5.1.3. 主成份分析的主要步驟
- 標準化數據集
- 建立共變數矩陣
- 從共變數矩陣分解出特徵值與特徵向量
- 以遞減方式對特徵值進行排序,以便對特徵向量排名
1: import pandas as pd 2: from sklearn.model_selection import train_test_split 3: from sklearn.preprocessing import StandardScaler 4: import numpy as np 5: import matplotlib.pyplot as plt 6: from sklearn.decomposition import PCA 7: 8: # ## 步驟式提取主成分(Principal Components) 9: 10: # 讀取葡萄酒數據集,數據來自UCI機器學習庫 11: # 這是一個多分類問題,目標是預測葡萄酒的種類(class label) 12: df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/' 13: 'machine-learning-databases/wine/wine.data', 14: header=None) 15: 16: # 設定資料欄位名稱 17: # 第一欄是類別標籤,其餘欄位是葡萄酒的各種特徵值 18: df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 19: 'Alcalinity of ash', 'Magnesium', 'Total phenols', 20: 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 21: 'Color intensity', 'Hue', 22: 'OD280/OD315 of diluted wines', 'Proline'] 23: 24: # 查看數據集的前五行 25: print(df_wine.head()) 26: 27: # 將數據分為特徵矩陣 X 和目標向量 y 28: # X 包含從第二列到最後一列的數據(特徵值) 29: # y 包含第一列的數據(類別標籤) 30: X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values 31: 32: # 將數據分為訓練集(70%)和測試集(30%) 33: # stratify=y 確保類別分佈在訓練集和測試集中大致相同 34: X_train, X_test, y_train, y_test = train_test_split(X, y, 35: test_size=0.3, 36: stratify=y, random_state=0) 37: 38: # 1. 對數據進行標準化處理 39: # 標準化是 PCA 的必要步驟,確保所有特徵值的範圍一致,避免尺度差異影響結果 40: sc = StandardScaler() 41: X_train_std = sc.fit_transform(X_train) # 使用訓練集計算均值與標準差,並標準化數據 42: X_test_std = sc.transform(X_test) # 使用訓練集的均值與標準差標準化測試集 43: 44: # 2. 計算共變數矩陣並進行特徵值分解(Eigendecomposition) 45: # 共變數矩陣用於衡量特徵之間的相關性 46: cov_mat = np.cov(X_train_std.T) # 計算轉置後數據的共變數矩陣 47: 48: # 計算特徵值(eigenvalues)和特徵向量(eigenvectors) 49: # 特徵值表示對應主成分的變異數,特徵向量表示主成分的方向 50: eigen_vals, eigen_vecs = np.linalg.eig(cov_mat) 51: 52: # 輸出特徵值,觀察各主成分的變異數 53: print('\nEigenvalues \n%s' % eigen_vals) 54: 55: # ## 計算總變異數與解釋變異數 56: 57: # 計算特徵值總和(即總變異數) 58: tot = sum(eigen_vals) 59: 60: # 計算各主成分解釋的變異數比例,並按從大到小排序 61: var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)] 62: 63: # 計算累積解釋變異數比例 64: cum_var_exp = np.cumsum(var_exp) 65: 66: # 繪製柱狀圖和階梯圖 67: # 柱狀圖顯示各主成分單獨解釋的變異數比例 68: # 階梯圖顯示累積解釋變異數比例 69: plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', 70: label='individual explained variance') 71: plt.step(range(1, 14), cum_var_exp, where='mid', 72: label='cumulative explained variance') 73: plt.ylabel('Explained variance ratio') # y 軸標籤:解釋變異數比例 74: plt.xlabel('Principal component index') # x 軸標籤:主成分索引 75: plt.legend(loc='best') # 顯示圖例 76: plt.tight_layout() # 自動調整布局 77: plt.savefig('05_02.png', dpi=300) # 保存圖片為高解析度 PNG 78: # plt.show() # 如果需要即時顯示圖表,可解除這行註解
Class label Alcohol ... OD280/OD315 of diluted wines Proline 0 1 14.23 ... 3.92 1065 1 1 13.20 ... 3.40 1050 2 1 13.16 ... 3.17 1185 3 1 14.37 ... 3.45 1480 4 1 13.24 ... 2.93 735 [5 rows x 14 columns] Eigenvalues [4.84274532 2.41602459 1.54845825 0.96120438 0.84166161 0.6620634 0.51828472 0.34650377 0.3131368 0.10754642 0.21357215 0.15362835 0.1808613 ]
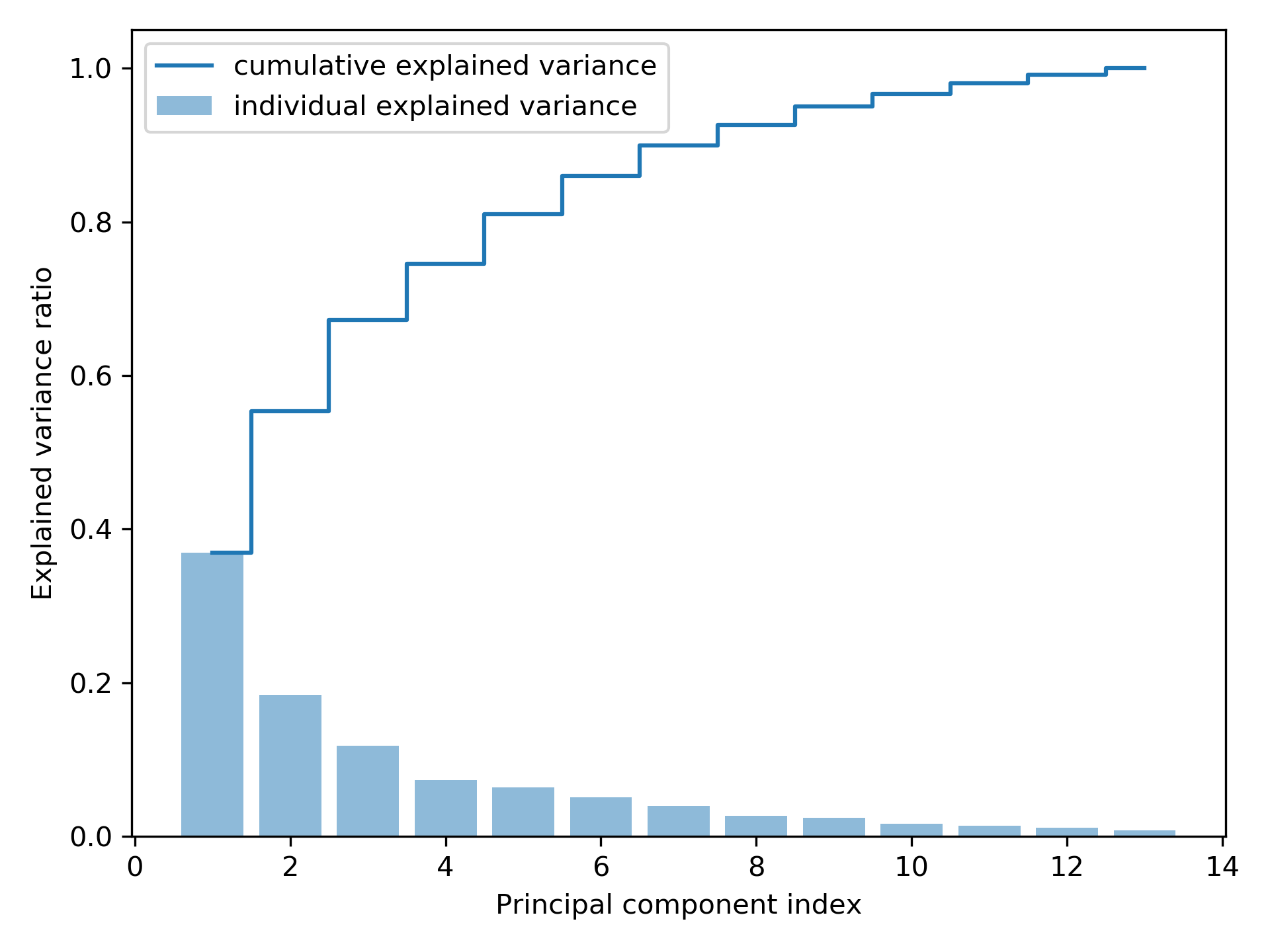
Figure 45: Principal component index
雖然上圖的「解釋變異數」圖有點類似隨機森林評估特徵值重要性的結果,但二者最大的不同處在於 PCA 為一種非監督式方法,也就是說,關於類別標籤資訊是被忽略的。
5.1.4. 特徵轉換
在分解「共變數矩陣」成為「特徵對」後,接下來要將資料集轉換為新的「主成份」,其步驟如下:
- 選取\(k\)個最大特徵值所對應的 k 個特徵向量,其中\(k\)為新「特徵空間」的維數(\(k \le d\))。
- 用最前面的\(k\)個特徵向量建立「投影矩陣」(project matrix)\(W\)。
- 使用投影矩陣\(W\),輸入值為\(d\)維數據集、輸出值為新的\(k\)維「特徵子空間」。
1: import pandas as pd 2: from sklearn.model_selection import train_test_split 3: from sklearn.preprocessing import StandardScaler 4: import numpy as np 5: import matplotlib.pyplot as plt 6: from sklearn.decomposition import PCA 7: 8: # ## Extracting the principal components step-by-step 9: 10: df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/' 11: 'machine-learning-databases/wine/wine.data', 12: header=None) 13: 14: # df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 15: # 'Alcalinity of ash', 'Magnesium', 'Total phenols', 16: # 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 17: # 'Color intensity', 'Hue', 18: # 'OD280/OD315 of diluted wines', 'Proline'] 19: 20: # Splitting the data into 70% training and 30% test subsets. 21: X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values 22: X_train, X_test, y_train, y_test = train_test_split(X, y, 23: test_size=0.3, 24: stratify=y, random_state=0) 25: # 1. Standardizing the data. 26: sc = StandardScaler() 27: X_train_std = sc.fit_transform(X_train) 28: X_test_std = sc.transform(X_test) 29: # 2. Eigendecomposition of the covariance matrix. 30: cov_mat = np.cov(X_train_std.T) 31: eigen_vals, eigen_vecs = np.linalg.eig(cov_mat) 32: # ## Total and explained variance 33: #tot = sum(eigen_vals) 34: #var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)] 35: #cum_var_exp = np.cumsum(var_exp) 36: # ## Feature transformation 37: # Make a list of (eigenvalue, eigenvector) tuples 38: eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) 39: for i in range(len(eigen_vals))] 40: # Sort the (eigenvalue, eigenvector) tuples from high to low 41: eigen_pairs.sort(key=lambda k: k[0], reverse=True) 42: w = np.hstack((eigen_pairs[0][1][:, np.newaxis], 43: eigen_pairs[1][1][:, np.newaxis])) 44: print('Matrix W:\n', w) 45: print(X_train_std[0].dot(w)) 46: X_train_pca = X_train_std.dot(w) 47: # plot 48: colors = ['r', 'b', 'g'] 49: markers = ['s', 'x', 'o'] 50: 51: for l, c, m in zip(np.unique(y_train), colors, markers): 52: plt.scatter(X_train_pca[y_train == l, 0], 53: X_train_pca[y_train == l, 1], 54: c=c, label=l, marker=m) 55: 56: plt.xlabel('PC 1') 57: plt.ylabel('PC 2') 58: plt.legend(loc='lower left') 59: plt.tight_layout() 60: plt.savefig('05_03.png', dpi=300) 61: #plt.show() 62:
Matrix W: [[-0.13724218 0.50303478] [ 0.24724326 0.16487119] [-0.02545159 0.24456476] [ 0.20694508 -0.11352904] [-0.15436582 0.28974518] [-0.39376952 0.05080104] [-0.41735106 -0.02287338] [ 0.30572896 0.09048885] [-0.30668347 0.00835233] [ 0.07554066 0.54977581] [-0.32613263 -0.20716433] [-0.36861022 -0.24902536] [-0.29669651 0.38022942]] [2.38299011 0.45458499]
使用上述程式碼產生的 13*2 維的投影矩陣可以轉換一個樣本\(x\)(以\(1 \times 13\)維的列向量表示)到 PCA 子空間(\(x'\))(前兩個主成份):\(x' = xW\)(程式碼第45行);同樣的,我們也可以將整個\(124 \times 13\)維的訓練數據集轉換到兩個主成份(\(124 \times 2\)維)(程式第46行),最後,將轉換過的\(124 \times 2\)維矩陣以二維散點圖表示:
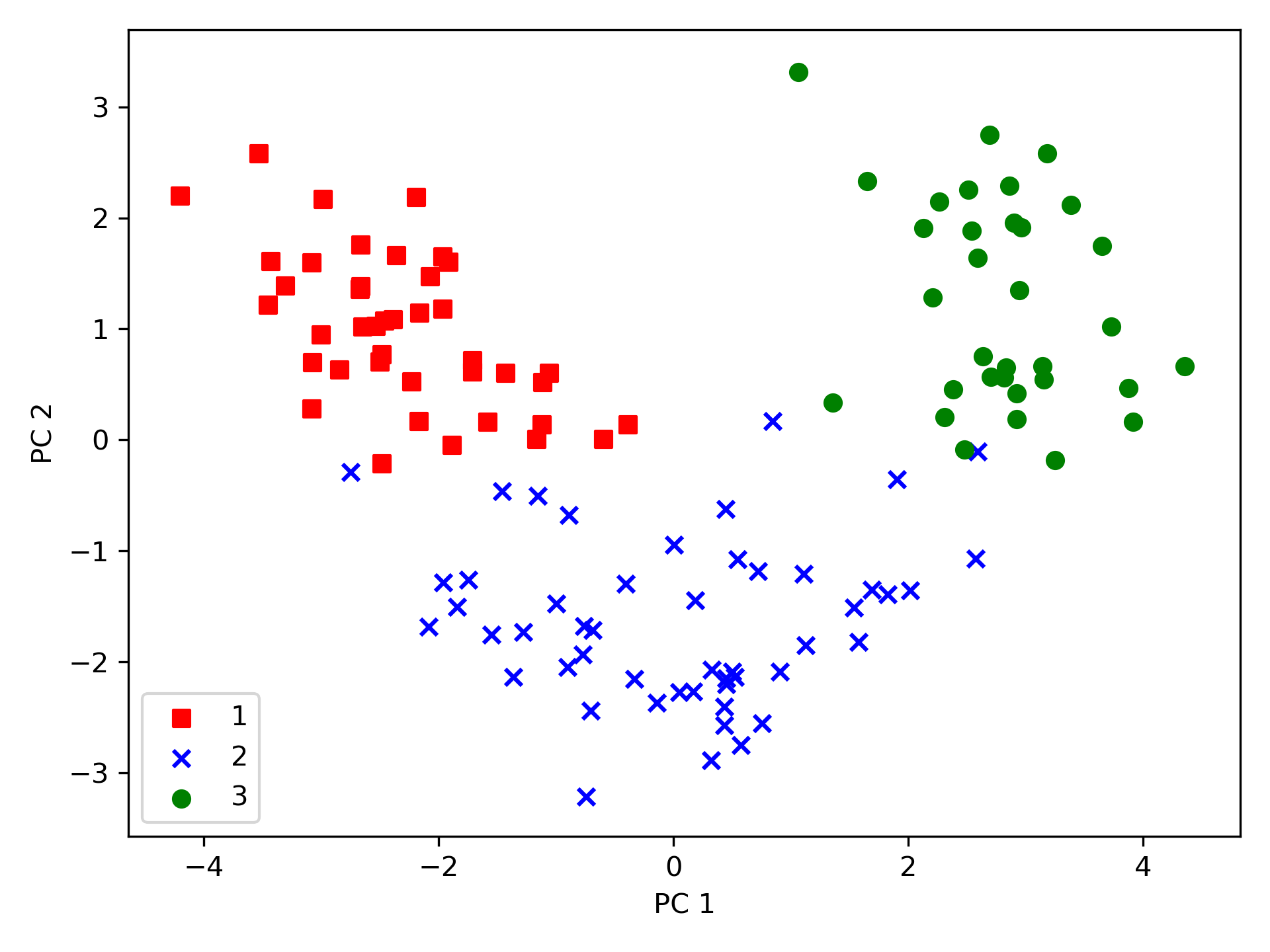
Figure 46: 05_03
由圖46中可看出,與第二個主成份(y 軸)相比,數據沿著第一主成份(x 軸)的分散程度更嚴重,而由此圖也可判斷,該數據應可以一個「線性分類器」進行有效分類。
5.1.5. 以 Scikit-learn 進行主成份分析
1: from matplotlib.colors import ListedColormap 2: import pandas as pd 3: from sklearn.model_selection import train_test_split 4: from sklearn.preprocessing import StandardScaler 5: import numpy as np 6: import matplotlib.pyplot as plt 7: from sklearn.decomposition import PCA 8: from sklearn.linear_model import LogisticRegression 9: 10: # ## Extracting the principal components step-by-step 11: 12: df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/' 13: 'machine-learning-databases/wine/wine.data', 14: header=None) 15: 16: # df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 17: # 'Alcalinity of ash', 'Magnesium', 'Total phenols', 18: # 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 19: # 'Color intensity', 'Hue', 20: # 'OD280/OD315 of diluted wines', 'Proline'] 21: 22: # Splitting the data into 70% training and 30% test subsets. 23: X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values 24: X_train, X_test, y_train, y_test = train_test_split(X, y, 25: test_size=0.3, 26: stratify=y, random_state=0) 27: # 1. Standardizing the data. 28: sc = StandardScaler() 29: X_train_std = sc.fit_transform(X_train) 30: X_test_std = sc.transform(X_test) 31: 32: def plot_decision_regions(X, y, classifier, resolution=0.02): 33: # setup marker generator and color map 34: markers = ('s', 'x', 'o', '^', 'v') 35: colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan') 36: cmap = ListedColormap(colors[:len(np.unique(y))]) 37: 38: # plot the decision surface 39: x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 40: x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 41: xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), 42: np.arange(x2_min, x2_max, resolution)) 43: Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) 44: Z = Z.reshape(xx1.shape) 45: plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) 46: plt.xlim(xx1.min(), xx1.max()) 47: plt.ylim(xx2.min(), xx2.max()) 48: 49: # plot class samples 50: for idx, cl in enumerate(np.unique(y)): 51: plt.scatter(x=X[y == cl, 0], 52: y=X[y == cl, 1], 53: alpha=0.6, 54: c=cmap(idx), 55: edgecolor='black', 56: marker=markers[idx], 57: label=cl) 58: 59: # Training logistic regression classifier using the first 2 principal components. 60: pca = PCA(n_components=2) 61: X_train_pca = pca.fit_transform(X_train_std) 62: X_test_pca = pca.transform(X_test_std) 63: 64: lr = LogisticRegression() 65: lr = lr.fit(X_train_pca, y_train) 66: 67: plot_decision_regions(X_train_pca, y_train, classifier=lr) 68: plt.xlabel('PC 1') 69: plt.ylabel('PC 2') 70: plt.legend(loc='lower left') 71: plt.tight_layout() 72: plt.savefig('05_04.png', dpi=300) 73: #plt.show() 74: plot_decision_regions(X_test_pca, y_test, classifier=lr) 75: plt.xlabel('PC 1') 76: plt.ylabel('PC 2') 77: plt.legend(loc='lower left') 78: plt.tight_layout() 79: plt.savefig('05_05.png', dpi=300) 80: #plt.show()
PCA 類別是 scikit-learn 中許多轉換類別之一,首先使用訓練數據集來 fit 模型並轉換數據集(程式第61行),最後以 Logistic 迴歸對數據進行分類。圖47為訓練集資料的分類結果,圖48測為測試資料集分類結果,可以看出二者差異不大。
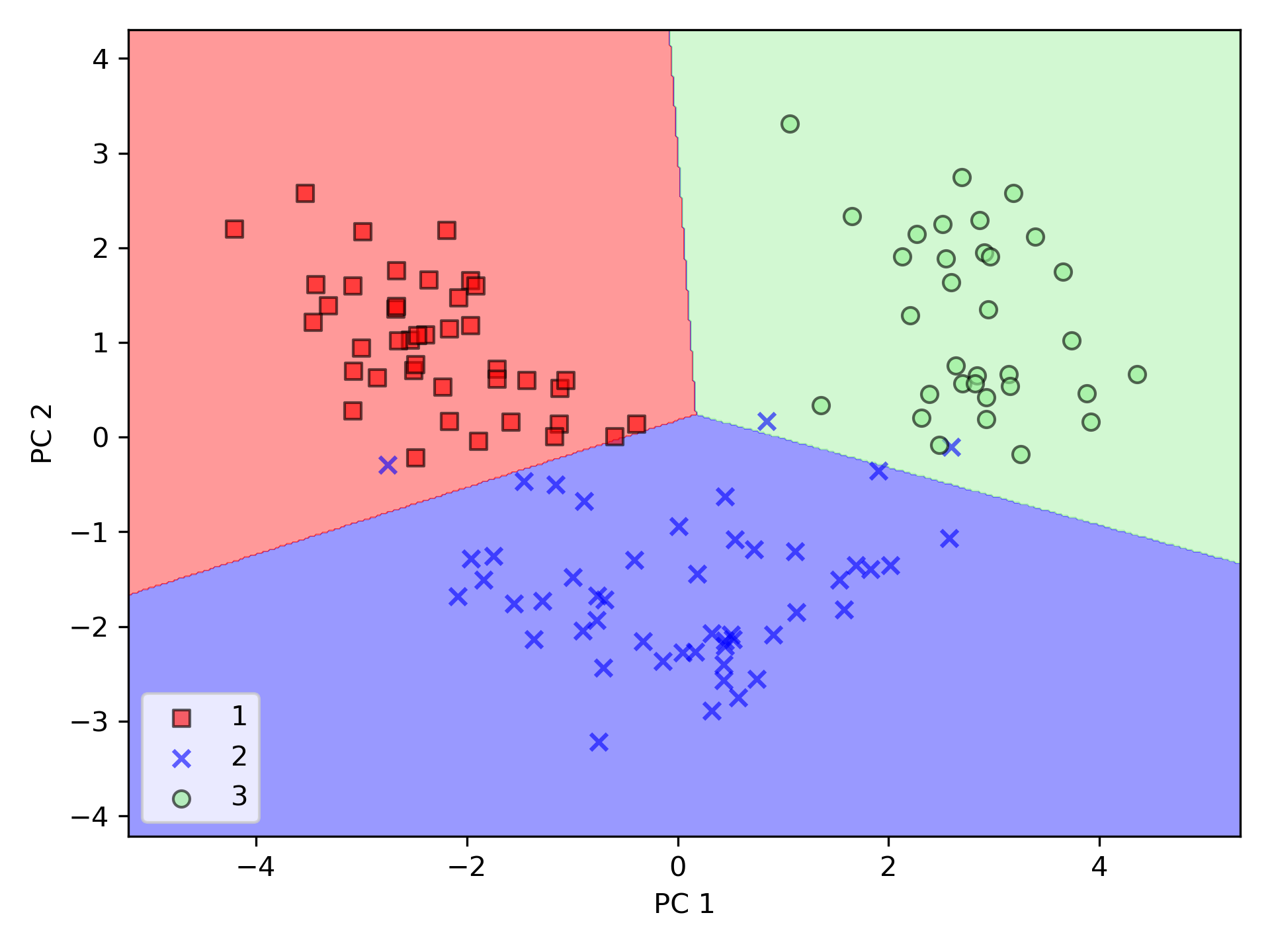
Figure 47: PCA 訓練數據
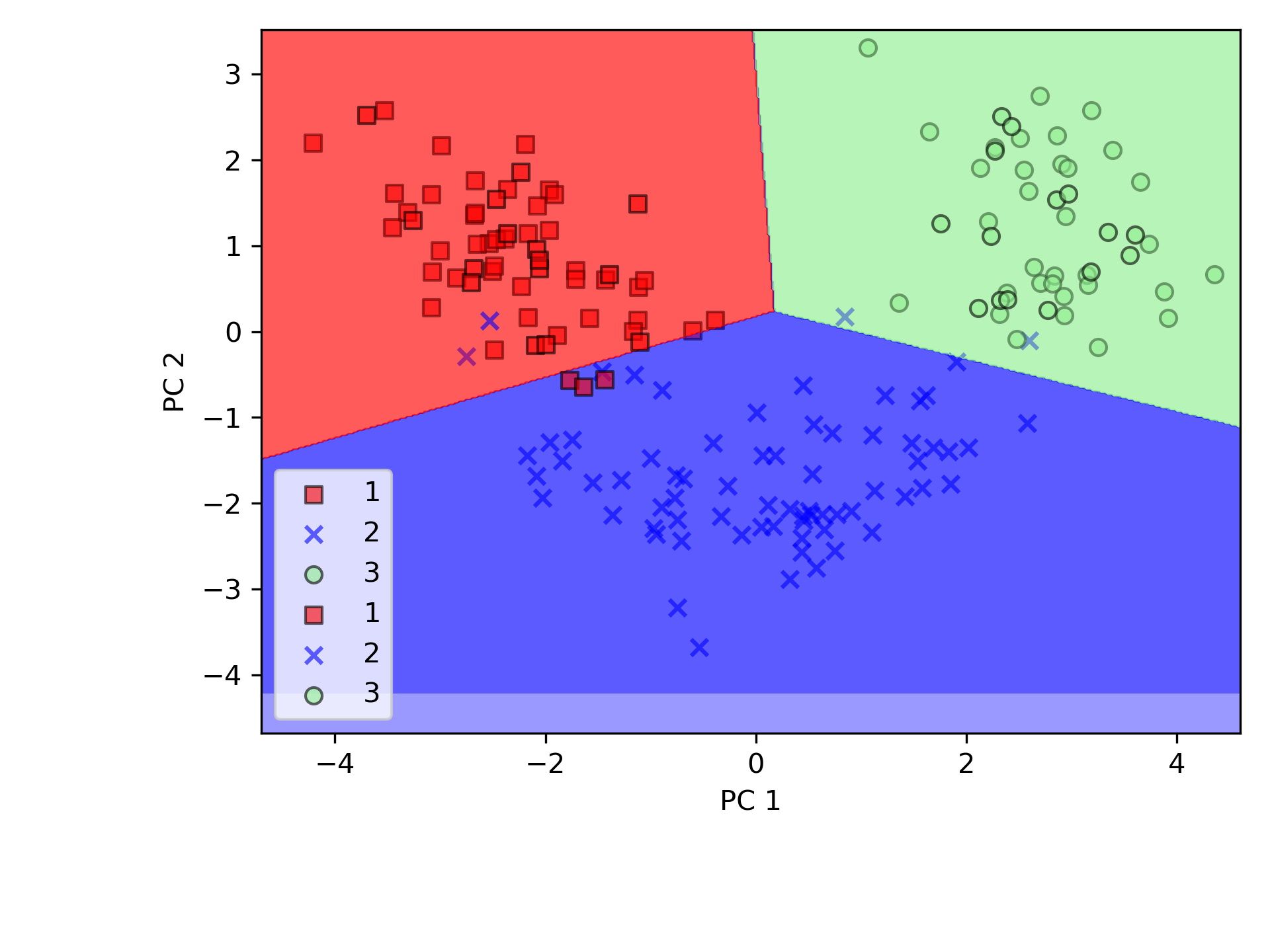
Figure 48: PCA 測試數據
5.2. 利用線性判別分析(LDA)做監督式數據壓縮
LDA 的全稱是 Linear Discriminant Analysis(線性判別分析),是一種 supervised learning。因為是由 Fisher 在 1936 年提出的,所以也叫 Fisher’s Linear Discriminant。「線性判別分析」(linear discriminant analysis, LDA)為一種用來做「特徵提取」的技術,藉由降維來處理「維數災難」,可提高非正規化模型的計算效率。PCA 在於找出一個在數據集中最大化變異數的正交成分軸; 而 LDA 則是要找出可以最佳化類別分離的特徵子空間。
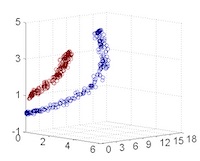
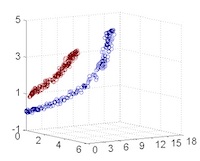
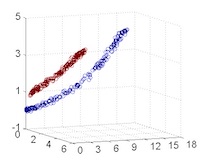
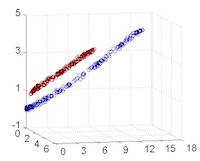
從主觀的理解上,主成分分析到底是什麼?它其實是對數據在高維空間下的一個投影轉換,通過一定的投影規則將原來從一個角度看到的多個維度映射成較少的維度。到底什麼是映射,下面的圖就可以很好地解釋這個問題——正常角度看是兩個半橢圓形分佈的數據集,但經過旋轉(映射)之後是兩條線性分佈數據集。4
 |
 |
 |
 |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
 |
 |
 |
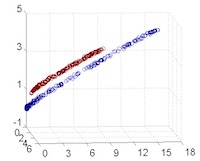 |
| 5 | 6 | 7 | 8 |
LDA 與 PCA 都是常用的降維方法,二者的區別在於4:
- 出發思想不同。PCA 主要是從特徵的協方差角度,去找到比較好的投影方式,即選擇樣本點投影具有最大方差的方向( 在信號處理中認為信號具有較大的方差,噪聲有較小的方差,信噪比就是信號與噪聲的方差比,越大越好。);而 LDA 則更多的是考慮了分類標籤信息,尋求投影后不同類別之間數據點距離更大化以及同一類別數據點距離最小化,即選擇分類性能最好的方向。
- 學習模式不同。PCA 屬於無監督式學習,因此大多場景下只作為數據處理過程的一部分,需要與其他算法結合使用,例如將 PCA 與聚類、判別分析、回歸分析等組合使用;LDA 是一種監督式學習方法,本身除了可以降維外,還可以進行預測應用,因此既可以組合其他模型一起使用,也可以獨立使用。
- 降維後可用維度數量不同。LDA 降維後最多可生成 C-1 維子空間(分類標籤數-1),因此 LDA 與原始維度 N 數量無關,只有數據標籤分類數量有關;而 PCA 最多有 n 維度可用,即最大可以選擇全部可用維度。
圖49左側是 PCA 的降維思想,它所作的只是將整組數據整體映射到最方便表示這組數據的坐標軸上,映射時沒有利用任何數據內部的分類信息。因此,雖然 PCA 後的數據在表示上更加方便(降低了維數並能最大限度的保持原有信息),但在分類上也許會變得更加困難;圖49右側是 LDA 的降維思想,可以看到 LDA 充分利用了數據的分類信息,將兩組數據映射到了另外一個坐標軸上,使得數據更易區分了(在低維上就可以區分,減少了運算量)。
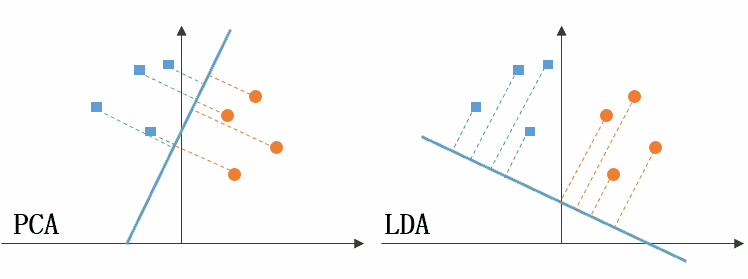
Figure 49: PCA LDA 差異
線性判別分析 LDA 算法由於其簡單有效性在多個領域都得到了廣泛地應用,是目前機器學習、數據挖掘領域經典且熱門的一個算法;但是算法本身仍然存在一些侷限性:
- 當樣本數量遠小於樣本的特徵維數,樣本與樣本之間的距離變大使得距離度量失效,使 LDA 算法中的類內、類間離散度矩陣奇異,不能得到最優的投影方向,在人臉識別領域中表現得尤為突出
- LDA 不適合對非高斯分佈的樣本進行降維
- LDA 在樣本分類信息依賴方差而不是均值時,效果不好
- LDA 可能過度擬合數據
6. 信用卡詐欺偵測
- 資料來源: Hands-On Unsupervised Learning Using Python: How to Build Applied Machine Learning Solutions from Ulabled Data
- Code: https://github.com/aapatel09/handson-unsupervised-learning/blob/master/02_end_to_end_machine_learning_project.ipynb
6.1. 資料取得
6.1.1. for Google colab
1: %mkdir "/content/drive/My Drive/403AI"
1: # Define functions to connect to Google and change directories 2: def connectDrive(): 3: from google.colab import drive 4: drive.mount('/content/drive', force_remount=True) 5: 6: def changeDirectory(path): 7: import os 8: original_path = os.getcwd() 9: os.chdir(path) 10: new_path = os.getcwd() 11: print("Original path: ",original_path) 12: print("New path: ",new_path) 13: 14: # Connect to Google Drive 15: connectDrive() 16: 17: # Change path 18: changeDirectory("/content/drive/My Drive/403AI/")
6.1.2. Import Libraries
1: '''Main''' 2: import numpy as np 3: import pandas as pd 4: import os 5: 6: '''Data 7: Viz''' 8: import matplotlib.pyplot as plt 9: import matplotlib as mpl 10: import seaborn as sns 11: color = sns.color_palette() 12: 13: #%matplotlib inline 14: '''Data Prep''' 15: from sklearn import preprocessing as pp 16: from scipy.stats import pearsonr 17: from sklearn.model_selection import train_test_split 18: from sklearn.model_selection import StratifiedKFold 19: from sklearn.metrics import log_loss 20: from sklearn.metrics import precision_recall_curve, average_precision_score 21: from sklearn.metrics import roc_curve, auc, roc_auc_score 22: from sklearn.metrics import confusion_matrix, classification_report 23: 24: '''Algos''' 25: from sklearn.linear_model import LogisticRegression 26: from sklearn.ensemble import RandomForestClassifier 27: # import xgboost as xgb 28: import lightgbm as lgb
6.2. 資料準備
6.2.1. 取得資料
1: # Acquire Data 2: data = pd.read_csv("https://media.githubusercontent.com/media/francis-kang/handson-unsupervised-learning/master/datasets/credit_card_data/credit_card.csv") 3: print(data)
Time V1 V2 V3 V4 V5 V6 V7 ... V23 V24 V25 V26 V27 V28 Amount Class
0 0.0 -1.359807 -0.072781 2.536347 1.378155 -0.338321 0.462388 0.239599 ... -0.110474 0.066928 0.128539 -0.189115 0.133558 -0.021053 149.62 0
1 0.0 1.191857 0.266151 0.166480 0.448154 0.060018 -0.082361 -0.078803 ... 0.101288 -0.339846 0.167170 0.125895 -0.008983 0.014724 2.69 0
2 1.0 -1.358354 -1.340163 1.773209 0.379780 -0.503198 1.800499 0.791461 ... 0.909412 -0.689281 -0.327642 -0.139097 -0.055353 -0.059752 378.66 0
3 1.0 -0.966272 -0.185226 1.792993 -0.863291 -0.010309 1.247203 0.237609 ... -0.190321 -1.175575 0.647376 -0.221929 0.062723 0.061458 123.50 0
4 2.0 -1.158233 0.877737 1.548718 0.403034 -0.407193 0.095921 0.592941 ... -0.137458 0.141267 -0.206010 0.502292 0.219422 0.215153 69.99 0
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
284802 172786.0 -11.881118 10.071785 -9.834783 -2.066656 -5.364473 -2.606837 -4.918215 ... 1.014480 -0.509348 1.436807 0.250034 0.943651 0.823731 0.77 0
284803 172787.0 -0.732789 -0.055080 2.035030 -0.738589 0.868229 1.058415 0.024330 ... 0.012463 -1.016226 -0.606624 -0.395255 0.068472 -0.053527 24.79 0
284804 172788.0 1.919565 -0.301254 -3.249640 -0.557828 2.630515 3.031260 -0.296827 ... -0.037501 0.640134 0.265745 -0.087371 0.004455 -0.026561 67.88 0
284805 172788.0 -0.240440 0.530483 0.702510 0.689799 -0.377961 0.623708 -0.686180 ... -0.163298 0.123205 -0.569159 0.546668 0.108821 0.104533 10.00 0
284806 172792.0 -0.533413 -0.189733 0.703337 -0.506271 -0.012546 -0.649617 1.577006 ... 0.376777 0.008797 -0.473649 -0.818267 -0.002415 0.013649 217.00 0
[284807 rows x 31 columns]
6.2.2. 資料探索
1: print(data.shape) 2: print(data.head(3)) 3: print(data.describe()) 4: print(data.columns)
(284807, 31)
Time V1 V2 V3 V4 ... V26 V27 V28 Amount Class
0 0.0 -1.359807 -0.072781 2.536347 1.378155 ... -0.189115 0.133558 -0.021053 149.62 0
1 0.0 1.191857 0.266151 0.166480 0.448154 ... 0.125895 -0.008983 0.014724 2.69 0
2 1.0 -1.358354 -1.340163 1.773209 0.379780 ... -0.139097 -0.055353 -0.059752 378.66 0
[3 rows x 31 columns]
Time V1 V2 ... V28 Amount Class
count 284807.000000 2.848070e+05 2.848070e+05 ... 2.848070e+05 284807.000000 284807.000000
mean 94813.859575 1.168375e-15 3.416908e-16 ... -1.227390e-16 88.349619 0.001727
std 47488.145955 1.958696e+00 1.651309e+00 ... 3.300833e-01 250.120109 0.041527
min 0.000000 -5.640751e+01 -7.271573e+01 ... -1.543008e+01 0.000000 0.000000
25% 54201.500000 -9.203734e-01 -5.985499e-01 ... -5.295979e-02 5.600000 0.000000
50% 84692.000000 1.810880e-02 6.548556e-02 ... 1.124383e-02 22.000000 0.000000
75% 139320.500000 1.315642e+00 8.037239e-01 ... 7.827995e-02 77.165000 0.000000
max 172792.000000 2.454930e+00 2.205773e+01 ... 3.384781e+01 25691.160000 1.000000
[8 rows x 31 columns]
Index(['Time', 'V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10',
'V11', 'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20',
'V21', 'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'Amount',
'Class'],
dtype='object')
找出非數值資料
1: import numpy as np 2: import pandas as pd 3: # data = pd.read_csv("./credit_card.csv") #直接從磁碟機中讀回 4: nanCounter = pd.isna(data).sum() #將np.isnan以pd.isna取代 5: print(nanCounter)
Time 0 V1 0 V2 0 V3 0 V4 0 V5 0 V6 0 V7 0 V8 0 V9 0 V10 0 V11 0 V12 0 V13 0 V14 0 V15 0 V16 0 V17 0 V18 0 V19 0 V20 0 V21 0 V22 0 V23 0 V24 0 V25 0 V26 0 V27 0 V28 0 Amount 0 Class 0 dtype: int64
找出缺漏值
1: distinctCounter = data.apply(lambda x: len(x.unique())) 2: print(distinctCounter)
Time 124592 V1 275663 V2 275663 V3 275663 V4 275663 V5 275663 V6 275663 V7 275663 V8 275663 V9 275663 V10 275663 V11 275663 V12 275663 V13 275663 V14 275663 V15 275663 V16 275663 V17 275663 V18 275663 V19 275663 V20 275663 V21 275663 V22 275663 V23 275663 V24 275663 V25 275663 V26 275663 V27 275663 V28 275663 Amount 32767 Class 2 dtype: int64
6.2.3. 建立feature matrix和labels array
1: # Generate feature matrix and labels array 2: dataX = data.copy().drop(['Class'],axis=1) 3: dataY = data['Class'].copy() 4: print(dataX.head(3)) 5: print(dataY.head(3))
Time V1 V2 V3 V4 V5 V6 V7 V8 ... V21 V22 V23 V24 V25 V26 V27 V28 Amount 0 0.0 -1.359807 -0.072781 2.536347 1.378155 -0.338321 0.462388 0.239599 0.098698 ... -0.018307 0.277838 -0.110474 0.066928 0.128539 -0.189115 0.133558 -0.021053 149.62 1 0.0 1.191857 0.266151 0.166480 0.448154 0.060018 -0.082361 -0.078803 0.085102 ... -0.225775 -0.638672 0.101288 -0.339846 0.167170 0.125895 -0.008983 0.014724 2.69 2 1.0 -1.358354 -1.340163 1.773209 0.379780 -0.503198 1.800499 0.791461 0.247676 ... 0.247998 0.771679 0.909412 -0.689281 -0.327642 -0.139097 -0.055353 -0.059752 378.66 [3 rows x 30 columns] 0 0 1 0 2 0 Name: Class, dtype: int64
6.2.4. 特徵工程與特徵選擇
1: correlationMatrix = pd.DataFrame(data=[],index=dataX.columns,columns=dataX.columns) 2: for i in dataX.columns: 3: for j in dataX.columns: 4: correlationMatrix.loc[i,j] = np.round(pearsonr(dataX.loc[:,i],dataX.loc[:,j])[0],2) 5: 6: count_classes = pd.value_counts(data['Class'],sort=True).sort_index() 7: ax = sns.barplot(x=count_classes.index, y=[tuple(count_classes/len(data))[0],tuple(count_classes/len(data))[1]]) 8: ax.set_title('Frequency Percentage by Class') 9: ax.set_xlabel('Class') 10: ax.set_ylabel('Frequency Percentage') 11: #plt.show() 12: plt.savefig('images/creditCardFreq.png', dpi=300)
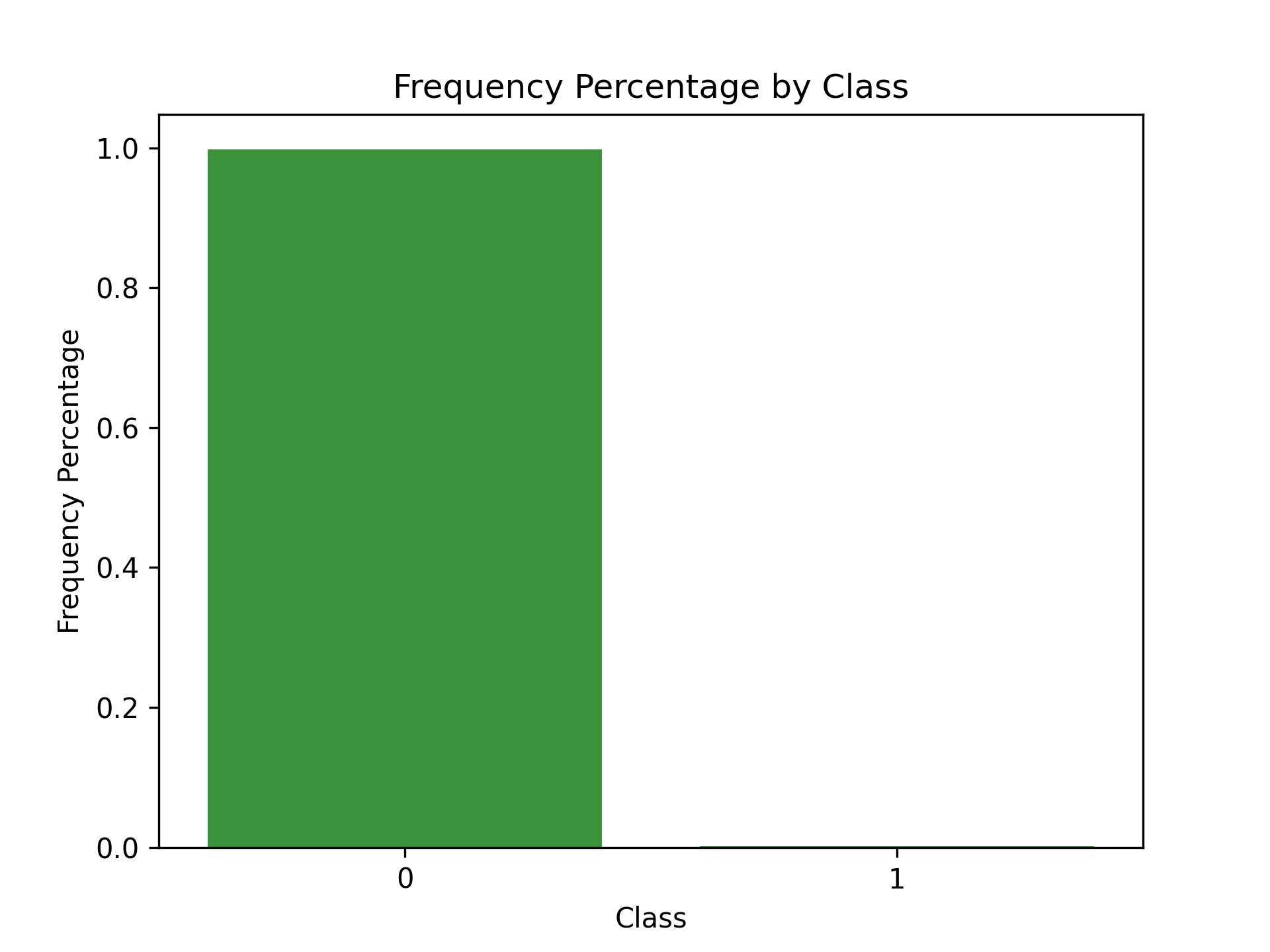
Figure 50: Frequency Percentage by Class
6.3. 模型準備
6.3.1. 切分訓練集與測試集
1: X_train, X_test, y_train, y_test = train_test_split(dataX, 2: dataY, test_size=0.33, 3: random_state=2018, stratify=dataY) 4: 5: print(len(X_train)) 6: print(len(X_test))
190820 93987
6.3.2. 選擇成本函數(loss function)
這是監督式分類問題,可以使用二元分類對數損失來計算實際label與模型預測二者間的交叉熵。 \[ log loss=-\frac{1}{N}\sum_{i=1}^N{\sum^M_{j=1}{y_{i,j}log(P_{i,j})} \] 其中
- N為資料數量
- M為label數量
- 若第 \(i\) 項為 \(j\) 類別, \(y_{i,j}\) 值為1,反之為0
- \(P_{i,j}\) 為預測類別項目 \(i\) 為 \(j\) 類別的機率
6.3.3. k-Fold交叉驗證
為了有效評估「模型演算法預測未曾見過的樣本」的表現成效,訓練集可再進一步拆成訓練集與驗證集,可以用 k-fold 交叉驗證來實作。
1: k_fold = StratifiedKFold(n_splits=5,shuffle=True,random_state=2018) 2: print(k_fold)
StratifiedKFold(n_splits=5, random_state=2018, shuffle=True)
6.3.4. Feature scaling
6.4. 模型訓練-1
先從最簡單的分類法做起:Logistic Regression分類
6.4.1. 模型1: Logistic Regression
- 懲罰項設為L2對離群值較不敏感,且會給全部特徵值分配非零權重,較為穩定;L1則會對最重要的特徵值分配最高權重,其他特徵值則給予接近零的權重,較不穩定。
- C為正規化的強度,正規化主要用來解決過度擬合的問題。C為一正浮點數,其值越小,正規化強度越強,預設值為1。
- 模型class_weight設為balanced,目的在告訴演算法這個訓練集的label類別分佈不平衡,在訓練時演算法就會對正向label加大權重。
1: #設定超參數 2: from sklearn.linear_model import LogisticRegression 3: penalty = 'l2' 4: C = 1.0 5: class_weight = 'balanced' 6: random_state = 2018 7: solver = 'liblinear' 8: n_jobs = 1 9: 10: logReg = LogisticRegression(penalty=penalty, C=C, 11: class_weight=class_weight, random_state=random_state, solver=solver, n_jobs=n_jobs) 12: print(logReg)
LogisticRegression(class_weight='balanced', n_jobs=1, random_state=2018,
solver='liblinear')
6.4.2. 訓練模型
1: trainingScores = [] 2: cvScores = [] 3: predictionsBasedOnKFolds = pd.DataFrame(data=[], index=y_train.index,columns=[0,1]) 4: 5: penalty = 'l2' 6: C = 1.0 7: class_weight = 'balanced' 8: random_state = 2018 9: solver = 'liblinear' 10: n_jobs = 1 11: k_fold = StratifiedKFold(n_splits=5,shuffle=True,random_state=2018) 12: 13: logReg = LogisticRegression(penalty=penalty, C=C, 14: class_weight=class_weight, random_state=random_state, solver=solver, n_jobs=n_jobs) 15: 16: model = logReg 17: print(model) 18: for train_index, cv_index in k_fold.split(np.zeros(len(X_train)),y_train.ravel()): 19: X_train_fold, X_cv_fold = X_train.iloc[train_index,:], X_train.iloc[cv_index,:] 20: y_train_fold, y_cv_fold = y_train.iloc[train_index], y_train.iloc[cv_index] 21: 22: model.fit(X_train_fold, y_train_fold) 23: loglossTraining = log_loss(y_train_fold, model.predict_proba(X_train_fold)[:,1]) 24: trainingScores.append(loglossTraining) 25: 26: predictionsBasedOnKFolds.loc[X_cv_fold.index,:] = model.predict_proba(X_cv_fold) 27: loglossCV = log_loss(y_cv_fold, predictionsBasedOnKFolds.loc[X_cv_fold.index,1]) 28: cvScores.append(loglossCV) 29: 30: print('Training Log Loss: ', loglossTraining) 31: print('CV Log Loss: ', loglossCV) 32: 33: loglossLogisticRegression = log_loss(y_train, predictionsBasedOnKFolds.loc[:,1]) 34: print('Logistic Regression Log Loss: ', loglossLogisticRegression)
LogisticRegression(class_weight='balanced', n_jobs=1, random_state=2018,
solver='liblinear')
Training Log Loss: 0.10954763675404679
CV Log Loss: 0.10872713310759863
Training Log Loss: 0.10468236808859577
CV Log Loss: 0.10407923786166381
Training Log Loss: 0.11571053800039245
CV Log Loss: 0.11812201922603925
Training Log Loss: 0.11574462696076625
CV Log Loss: 0.11833216026592738
Training Log Loss: 0.09716362850332248
CV Log Loss: 0.09707807427732842
Logistic Regression Log Loss: 0.10926772494771149
6.4.3. 完整版程式碼(trainCreditCard-1.py)
1: #!/usr/bin/env python3 2: '''Main''' 3: import numpy as np 4: import pandas as pd 5: import os 6: 7: '''Data Viz''' 8: import matplotlib.pyplot as plt 9: import matplotlib as mpl 10: import seaborn as sns 11: color = sns.color_palette() 12: 13: #%matplotlib inline 14: 15: '''Data Prep''' 16: from sklearn import preprocessing as pp 17: from scipy.stats import pearsonr 18: from sklearn.model_selection import train_test_split 19: from sklearn.model_selection import StratifiedKFold 20: from sklearn.metrics import log_loss 21: from sklearn.metrics import precision_recall_curve, average_precision_score 22: from sklearn.metrics import roc_curve, auc, roc_auc_score 23: from sklearn.metrics import confusion_matrix, classification_report 24: 25: '''Algos''' 26: from sklearn.linear_model import LogisticRegression 27: from sklearn.ensemble import RandomForestClassifier 28: # import xgboost as xgb 29: #import lightgbm as lgb 30: 31: 32: data = pd.read_csv("./credit_card.csv") 33: nanCounter = pd.isna(data).sum() #將np.isnan以pd.isna取代 34: 35: dataX = data.copy().drop(['Class'],axis=1) 36: dataY = data['Class'].copy() 37: 38: X_train, X_test, y_train, y_test = train_test_split(dataX, 39: dataY, test_size=0.33, 40: random_state=2018, stratify=dataY) 41: 42: k_fold = StratifiedKFold(n_splits=5,shuffle=True,random_state=2018) 43: 44: from sklearn.linear_model import LogisticRegression 45: penalty = 'l2' 46: C = 1.0 47: class_weight = 'balanced' 48: random_state = 2018 49: solver = 'liblinear' 50: n_jobs = 1 51: 52: logReg = LogisticRegression(penalty=penalty, C=C, 53: class_weight=class_weight, random_state=random_state, solver=solver, n_jobs=n_jobs) 54: 55: trainingScores = [] 56: cvScores = [] 57: predictionsBasedOnKFolds = pd.DataFrame(data=[], index=y_train.index,columns=[0,1]) 58: 59: model = logReg 60: print(model) 61: for train_index, cv_index in k_fold.split(np.zeros(len(X_train)),y_train.ravel()): 62: X_train_fold, X_cv_fold = X_train.iloc[train_index,:], X_train.iloc[cv_index,:] 63: y_train_fold, y_cv_fold = y_train.iloc[train_index], y_train.iloc[cv_index] 64: 65: model.fit(X_train_fold, y_train_fold) 66: loglossTraining = log_loss(y_train_fold, model.predict_proba(X_train_fold)[:,1]) 67: trainingScores.append(loglossTraining) 68: 69: predictionsBasedOnKFolds.loc[X_cv_fold.index,:] = model.predict_proba(X_cv_fold) 70: loglossCV = log_loss(y_cv_fold, predictionsBasedOnKFolds.loc[X_cv_fold.index,1]) 71: cvScores.append(loglossCV) 72: 73: print('Training Log Loss: ', loglossTraining) 74: print('CV Log Loss: ', loglossCV) 75: 76: loglossLogisticRegression = log_loss(y_train, predictionsBasedOnKFolds.loc[:,1]) 77: print('Logistic Regression Log Loss: ', loglossLogisticRegression) 78:
LogisticRegression(class_weight='balanced', n_jobs=1, random_state=2018,
solver='liblinear')
Training Log Loss: 0.10939361490760419
CV Log Loss: 0.10853402466643607
Training Log Loss: 0.10453309543196382
CV Log Loss: 0.10404365007856392
Training Log Loss: 0.11558188743919326
CV Log Loss: 0.11799026783957066
Training Log Loss: 0.11560666592384615
CV Log Loss: 0.11818686208380477
Training Log Loss: 0.09707169357423985
CV Log Loss: 0.0969591251780277
Logistic Regression Log Loss: 0.10914278596928062
正常而言,Training Log Loss應該會略低於CV Log Loss,二者的值相近,表示未發生過擬合狀況(Training Log Loss很低但CV Log Loss很高)。
6.5. 評估指標
- 召回率(recall): 找出了幾筆在訓練集中的詐欺交易?
- 精確率(precision): 被模型標示為詐欺的交易中,有幾筆為真的詐欺交易
6.5.1. 混淆矩陣(Confusion Matrix)
此例的label分類高度不平衡,使用混淆矩陣意義不大。若預測所有的交易均非詐欺,則結果會有284315筆真陰性、492筆偽陰性、0筆真陽性、0筆偽陽性,精確度為0。
6.5.2. 精確率-召回率曲線
對於類別不平衡的資料集,比較好的效能評估方案為精準率與召回率。
6.5.3. precision=真陽性個數/(真陽性個數+偽陽性個數)
即,所有的陽性預測中,有多少是對的預測?
6.5.4. recall=真陽性個數/(真陽性個數+偽陰性個數)
即,模型能捕捉到多少個詐欺交易?
6.5.5. 取捨
- 高recall低precision: 雖然預測中會有很多真的詐欺,但也會出現太多誤判
- 低precision高recall: 因為標記許多詐欺案例,因此能捕捉到許多詐欺交易,但也有許多被詐欺交易的case並不是真的詐欺
- 權衡:precision-recall curve,可以在每個門檻值下計算出最佳的average precision
6.5.6. 接收者操作特徵(Receiver Operating Characteristic)
ROC將真陽性率當Y軸、將偽陽性率當X軸,真陽性率也可以被當成敏感度,而偽陽性率也可以被當作l-specificity。
1: preds = pd.concat([y_train,predictionsBasedOnKFolds.loc[:,1]], axis=1) 2: preds.columns = ['trueLabel','prediction'] 3: predictionsBasedOnKFoldsLogisticRegression = preds.copy() 4: 5: precision, recall, thresholds = precision_recall_curve(preds['trueLabel'], 6: preds['prediction']) 7: average_precision = average_precision_score(preds['trueLabel'], 8: preds['prediction']) 9: plt.figure() 10: plt.step(recall, precision, color='k', alpha=0.7, where='post') 11: plt.fill_between(recall, precision, step='post', alpha=0.3, color='k') 12: 13: plt.xlabel('Recall') 14: plt.ylabel('Precision') 15: plt.ylim([0.0, 1.05]) 16: plt.xlim([0.0, 1.0]) 17: plt.title('Precision-Recall curve: Average Precision = {0:0.2f}'.format(average_precision)) 18: plt.savefig('images/prec-recall.png', dpi=300) 19: fpr, tpr, thresholds = roc_curve(preds['trueLabel'],preds['prediction']) 20: areaUnderROC = auc(fpr, tpr) 21: 22: plt.figure() 23: plt.plot(fpr, tpr, color='r', lw=2, label='ROC curve') 24: plt.plot([0, 1], [0, 1], color='k', lw=2, linestyle='--') 25: plt.xlim([0.0, 1.0]) 26: plt.ylim([0.0, 1.05]) 27: plt.xlabel('False Positive Rate') 28: plt.ylabel('True Positive Rate') 29: plt.title('Receiver operating characteristic: \ 30: Area under the curve = {0:0.2f}'.format(areaUnderROC)) 31: plt.legend(loc="lower right") 32: plt.savefig('images/auROC.png', dpi=300) 33:
由圖51可以看出此模型能達到近80%的recall(捕捉到了80%的詐欺交易),以及近乎70%的precision(所有被標記為詐欺的case中,有70%為真的詐欺,但仍有30$交易被不正確的標記為詐欺)
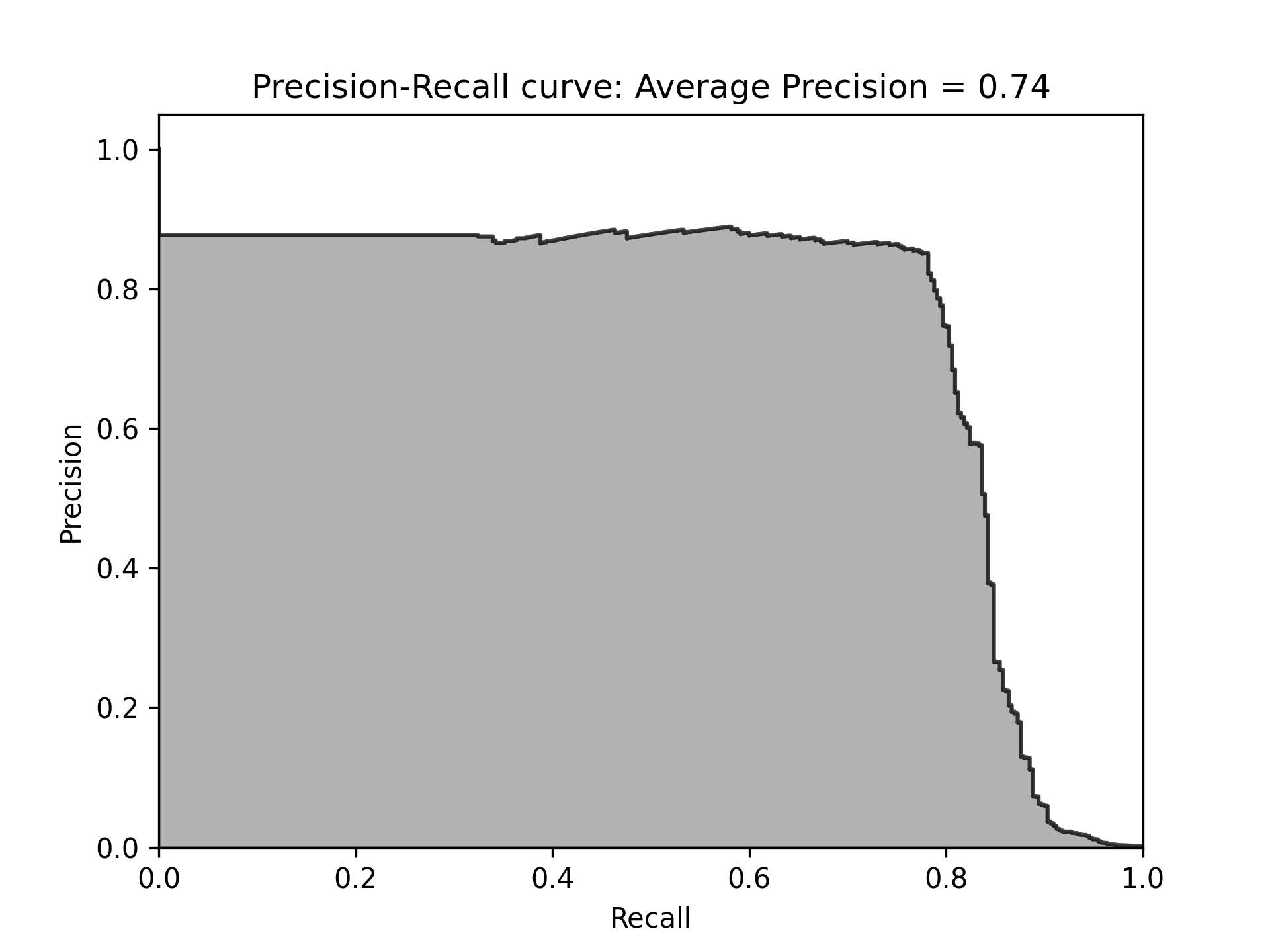
Figure 51: 模型Recall
圖52的auROC曲線允許我們在盡可能保持偽陽率低的情況下,決定有多少的詐欺案例能被捕捉到。
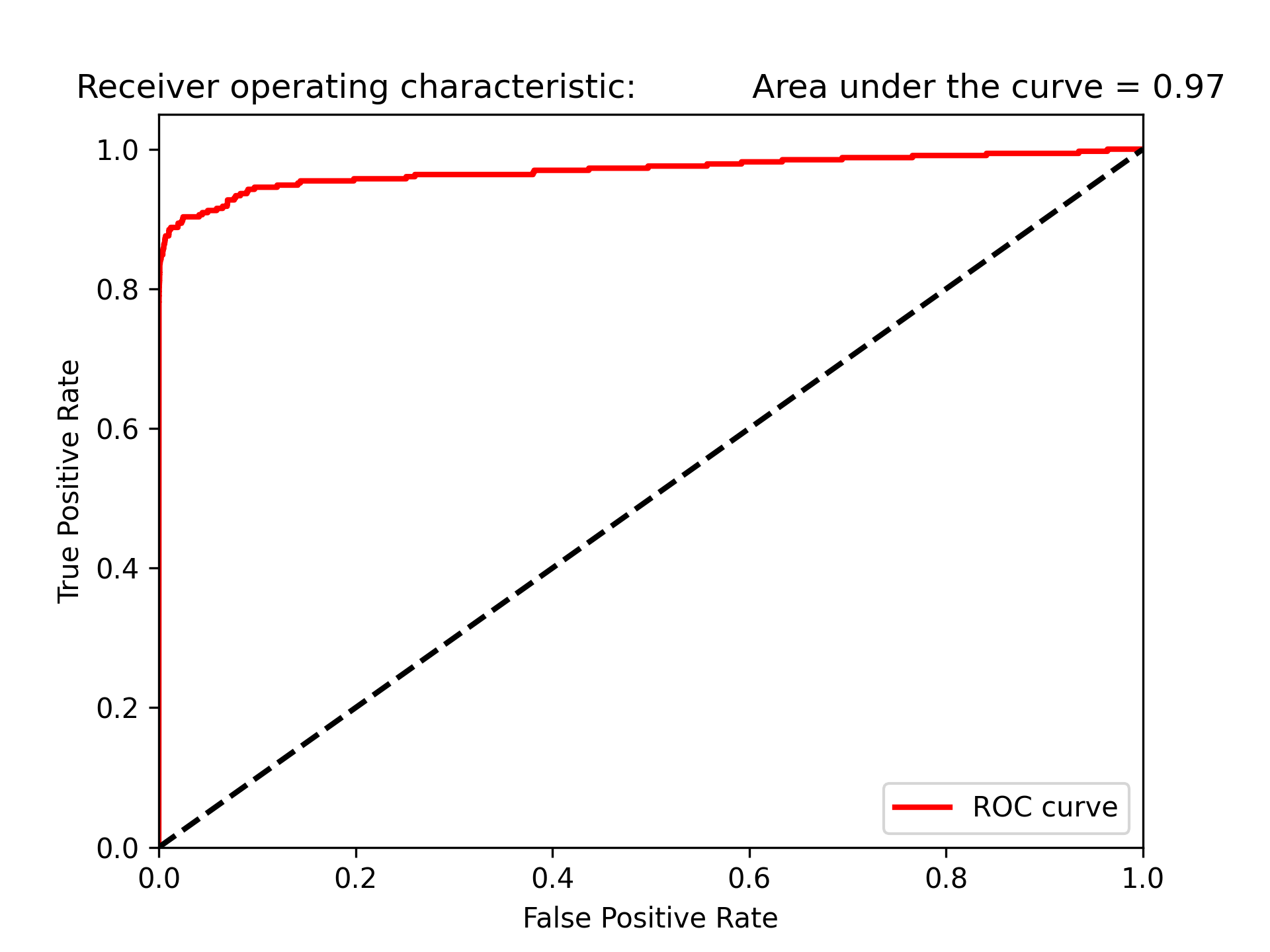
Figure 52: 模型auROC
6.6. 模型訓練#2
6.6.1. 模型#2: 隨機森林
設定超參數
- n_estimators = 10: 建立十顆樹並將這十顆樹的預測結果平均
- 這個case有30個特徵值,每顆樹會取總特徵值數的平方根值作為特徵數量,此例每顆樹會取5個特徵值
1: n_estimators = 10 2: max_features = 'auto' 3: max_depth = None 4: min_samples_split = 2 5: min_samples_leaf = 1 6: min_weight_fraction_leaf = 0.0 7: max_leaf_nodes = None 8: bootstrap = True 9: oob_score = False 10: n_jobs = -1 11: random_state = 2018 12: class_weight = 'balanced' 13: 14: RFC = RandomForestClassifier(n_estimators=n_estimators, 15: max_features=max_features, max_depth=max_depth, 16: min_samples_split=min_samples_split, min_samples_leaf=min_samples_leaf, 17: min_weight_fraction_leaf=min_weight_fraction_leaf, 18: max_leaf_nodes=max_leaf_nodes, bootstrap=bootstrap, 19: oob_score=oob_score, n_jobs=n_jobs, random_state=random_state, 20: class_weight=class_weight)
訓練模型
執行k-fold交叉驗證五次,每次用4/5訓練集做為訓練、1/5作為預測
1: trainingScores = [] 2: cvScores = [] 3: predictionsBasedOnKFolds = pd.DataFrame(data=[], 4: index=y_train.index,columns=[0,1]) 5: 6: model = RFC 7: 8: for train_index, cv_index in k_fold.split(np.zeros(len(X_train)), 9: y_train.ravel()): 10: X_train_fold, X_cv_fold = X_train.iloc[train_index,:], \ 11: X_train.iloc[cv_index,:] 12: y_train_fold, y_cv_fold = y_train.iloc[train_index], \ 13: y_train.iloc[cv_index] 14: 15: model.fit(X_train_fold, y_train_fold) 16: loglossTraining = log_loss(y_train_fold, \ 17: model.predict_proba(X_train_fold)[:,1]) 18: trainingScores.append(loglossTraining) 19: 20: predictionsBasedOnKFolds.loc[X_cv_fold.index,:] = \ 21: model.predict_proba(X_cv_fold) 22: loglossCV = log_loss(y_cv_fold, \ 23: predictionsBasedOnKFolds.loc[X_cv_fold.index,1]) 24: cvScores.append(loglossCV) 25: 26: print('Training Log Loss: ', loglossTraining) 27: print('CV Log Loss: ', loglossCV) 28: 29: loglossRandomForestsClassifier = log_loss(y_train, 30: predictionsBasedOnKFolds.loc[:,1]) 31: print('Random Forests Log Loss: ', loglossRandomForestsClassifier)
be675c0e-a262-4fe5-9b43-d9beaead1590
- 可以看出Training Log Loss明顯低於CV Log Loss,表示可能有過擬合的現象
- 但這兩個Loss指標仍明顯優於Logistic Regression模型(大概為後者的1/10)
評估結果
1: plt.cla() 2: preds = pd.concat([y_train,predictionsBasedOnKFolds.loc[:,1]], axis=1) 3: preds.columns = ['trueLabel','prediction'] 4: predictionsBasedOnKFoldsRandomForests = preds.copy() 5: 6: precision, recall, thresholds = precision_recall_curve(preds['trueLabel'], 7: preds['prediction']) 8: average_precision = average_precision_score(preds['trueLabel'], 9: preds['prediction']) 10: 11: plt.step(recall, precision, color='k', alpha=0.7, where='post') 12: plt.fill_between(recall, precision, step='post', alpha=0.3, color='k') 13: 14: plt.xlabel('Recall') 15: plt.ylabel('Precision') 16: plt.ylim([0.0, 1.05]) 17: plt.xlim([0.0, 1.0]) 18: 19: plt.title('Precision-Recall curve: Average Precision = {0:0.2f}'.format( 20: average_precision)) 21: plt.savefig('images/prec-recall-2.png', dpi=300) 22: 23: fpr, tpr, thresholds = roc_curve(preds['trueLabel'],preds['prediction']) 24: areaUnderROC = auc(fpr, tpr) 25: 26: plt.figure() 27: plt.plot(fpr, tpr, color='r', lw=2, label='ROC curve') 28: plt.plot([0, 1], [0, 1], color='k', lw=2, linestyle='--') 29: plt.xlim([0.0, 1.0]) 30: plt.ylim([0.0, 1.05]) 31: plt.xlabel('False Positive Rate') 32: plt.ylabel('True Positive Rate') 33: plt.title('Receiver operating characteristic: \ 34: Area under the curve = {0:0.2f}'.format( 35: areaUnderROC)) 36: plt.legend(loc="lower right") 37: plt.savefig('images/auROC-2.png', dpi=300)
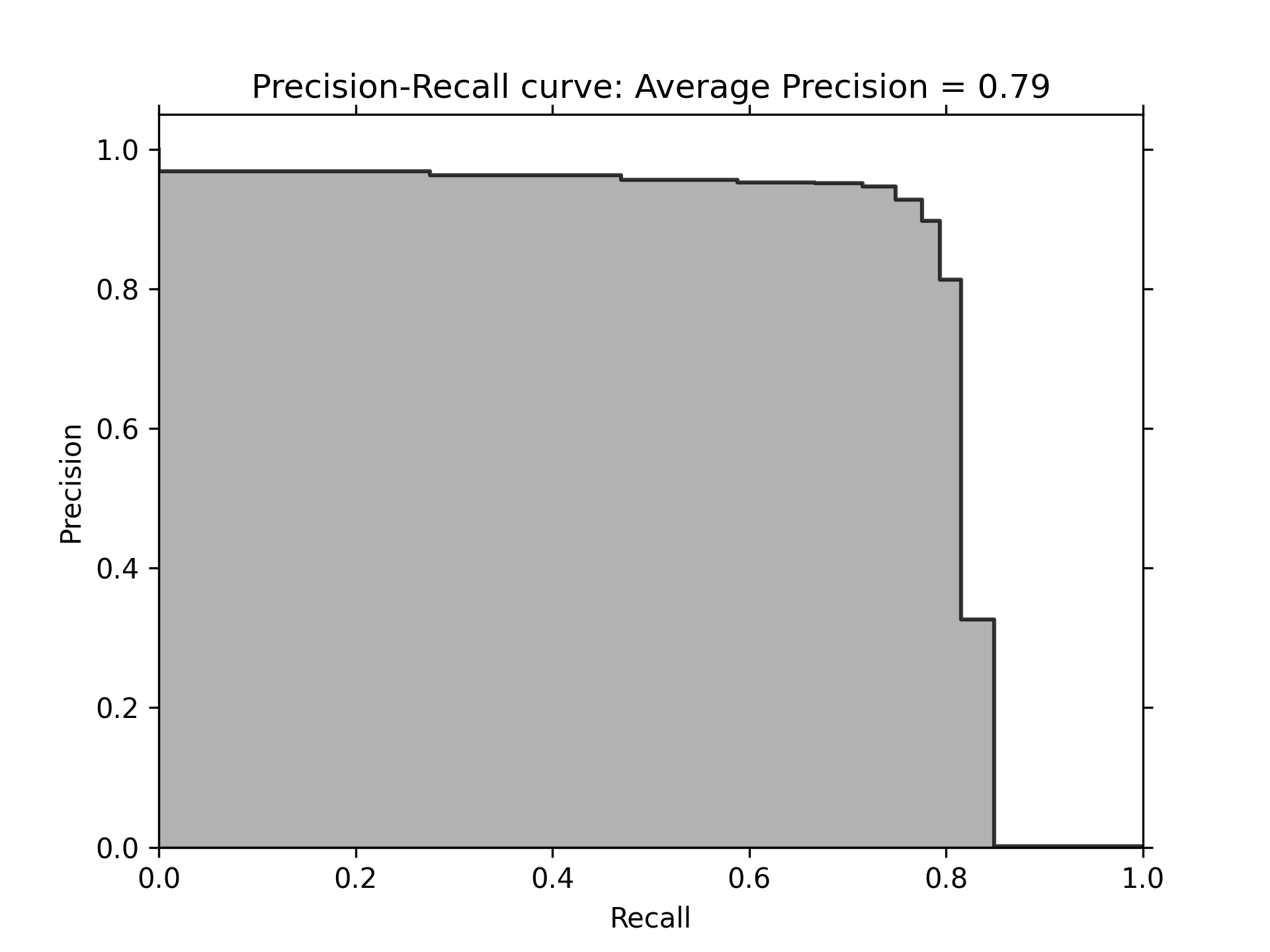
Figure 53: Caption
- 但隨機森林的auROC為0.92,不如Logistic Regression模型的0.97
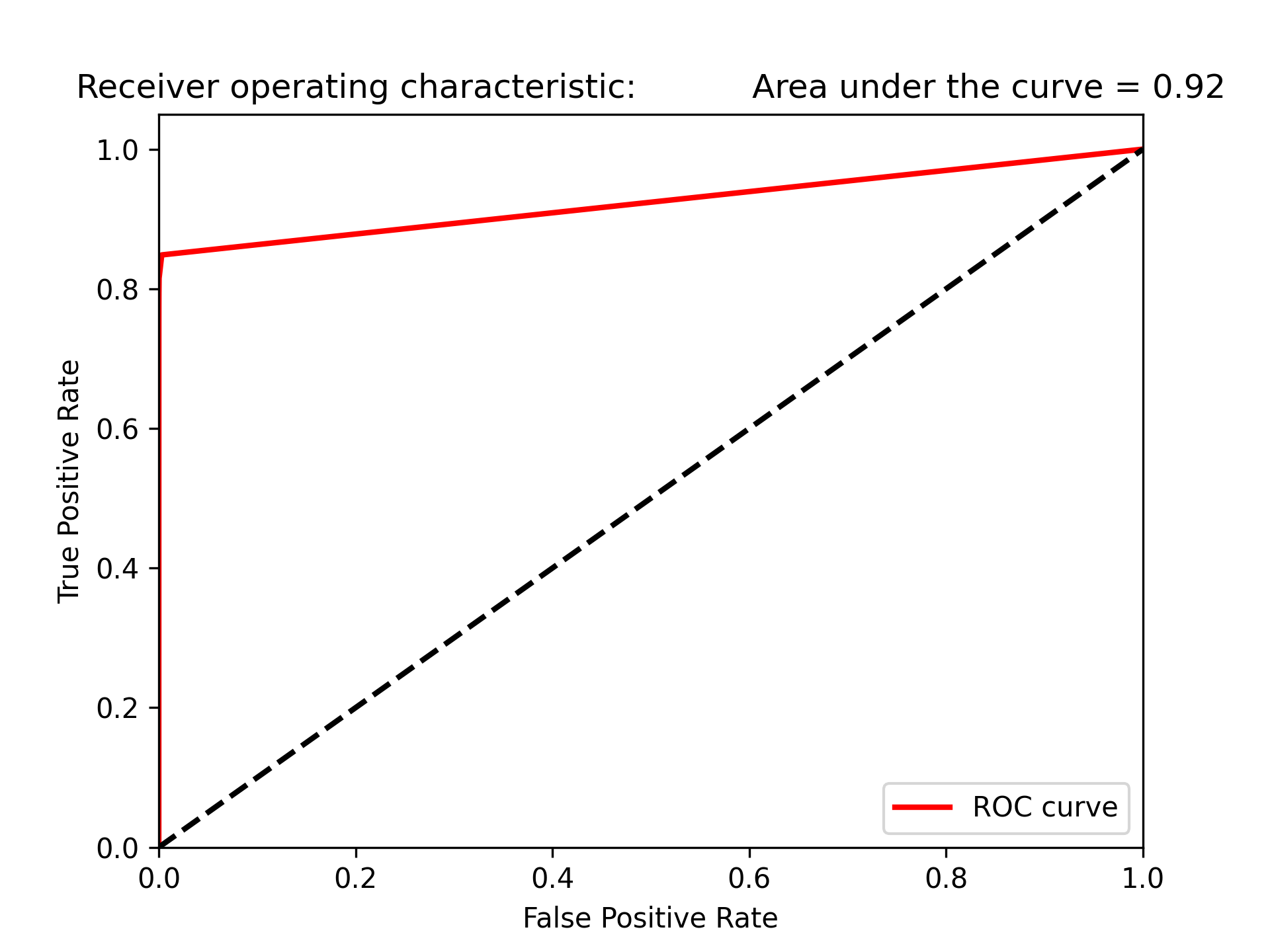
Figure 54: Caption
6.6.2. 模型#4: Gradient Boosting Machine (LightGBM)
讀資料
1: '''Main''' 2: import numpy as np 3: import pandas as pd 4: import os 5: 6: '''Data Viz''' 7: import matplotlib.pyplot as plt 8: import matplotlib as mpl 9: import seaborn as sns 10: color = sns.color_palette() 11: 12: #%matplotlib inline 13: 14: '''Data Prep''' 15: from sklearn import preprocessing as pp 16: from scipy.stats import pearsonr 17: from sklearn.model_selection import train_test_split 18: from sklearn.model_selection import StratifiedKFold 19: from sklearn.metrics import log_loss 20: from sklearn.metrics import precision_recall_curve, average_precision_score 21: from sklearn.metrics import roc_curve, auc, roc_auc_score 22: from sklearn.metrics import confusion_matrix, classification_report 23: 24: '''Algos''' 25: from sklearn.linear_model import LogisticRegression 26: from sklearn.ensemble import RandomForestClassifier 27: import xgboost as xgb 28: import lightgbm as lgb 29: 30: 31: #data = pd.read_csv("./credit_card.csv") 32: data = pd.read_csv("https://media.githubusercontent.com/media/francis-kang/handson-unsupervised-learning/master/datasets/credit_card_data/credit_card.csv") 33: nanCounter = pd.isna(data).sum() #將np.isnan以pd.isna取代 34: 35: dataX = data.copy().drop(['Class'],axis=1) 36: dataY = data['Class'].copy() 37: 38: X_train, X_test, y_train, y_test = train_test_split(dataX, 39: dataY, test_size=0.33, 40: random_state=2018, stratify=dataY) 41: 42: k_fold = StratifiedKFold(n_splits=5,shuffle=True,random_state=2018) 43:
設定超參數
1: params_lightGB = { 2: 'task': 'train', 3: 'num_class':1, 4: 'boosting': 'gbdt', 5: 'objective': 'binary', 6: 'metric': 'binary_logloss', 7: 'metric_freq':50, 8: 'is_training_metric':False, 9: 'max_depth':4, 10: 'num_leaves': 31, 11: 'learning_rate': 0.01, 12: 'feature_fraction': 1.0, 13: 'bagging_fraction': 1.0, 14: 'bagging_freq': 0, 15: 'bagging_seed': 2018, 16: 'verbose': -1, 17: 'num_threads':16 18: }
訓練模型
1: 2: trainingScores = [] 3: cvScores = [] 4: predictionsBasedOnKFolds = pd.DataFrame(data=[], 5: index=y_train.index,columns=['prediction']) 6: 7: for train_index, cv_index in k_fold.split(np.zeros(len(X_train)), 8: y_train.ravel()): 9: X_train_fold, X_cv_fold = X_train.iloc[train_index,:], \ 10: X_train.iloc[cv_index,:] 11: y_train_fold, y_cv_fold = y_train.iloc[train_index], \ 12: y_train.iloc[cv_index] 13: 14: lgb_train = lgb.Dataset(X_train_fold, y_train_fold) 15: lgb_eval = lgb.Dataset(X_cv_fold, y_cv_fold, reference=lgb_train) 16: gbm = lgb.train(params_lightGB, lgb_train, num_boost_round=2000, 17: valid_sets=lgb_eval) 18: 19: loglossTraining = log_loss(y_train_fold, \ 20: gbm.predict(X_train_fold, num_iteration=gbm.best_iteration)) 21: trainingScores.append(loglossTraining) 22: 23: predictionsBasedOnKFolds.loc[X_cv_fold.index,'prediction'] = \ 24: gbm.predict(X_cv_fold, num_iteration=gbm.best_iteration) 25: loglossCV = log_loss(y_cv_fold, \ 26: predictionsBasedOnKFolds.loc[X_cv_fold.index,'prediction']) 27: cvScores.append(loglossCV) 28: 29: print('Training Log Loss: ', loglossTraining) 30: print('CV Log Loss: ', loglossCV) 31: 32: loglossLightGBMGradientBoosting = \ 33: log_loss(y_train, predictionsBasedOnKFolds.loc[:,'prediction']) 34: print('LightGBM Gradient Boosting Log Loss: ', loglossLightGBMGradientBoosting)
Training Log Loss: 5.722067577767659e-05 CV Log Loss: 0.0028905982750420615 Training Log Loss: 5.326493165009444e-05 CV Log Loss: 0.00341349889324051 Training Log Loss: 6.167817302035956e-05 CV Log Loss: 0.0026930532519383577 Training Log Loss: 6.96104776294407e-05 CV Log Loss: 0.0029882236623969124 Training Log Loss: 5.316601718227403e-05 CV Log Loss: 0.004136416692029885 LightGBM Gradient Boosting Log Loss: 0.0032243581549295445
評估結果
1: plt.cla() 2: preds = pd.concat([y_train,predictionsBasedOnKFolds.loc[:,'prediction']], axis=1) 3: preds.columns = ['trueLabel','prediction'] 4: predictionsBasedOnKFoldsLightGBMGradientBoosting = preds.copy() 5: 6: precision, recall, thresholds = \ 7: precision_recall_curve(preds['trueLabel'],preds['prediction']) 8: average_precision = \ 9: average_precision_score(preds['trueLabel'],preds['prediction']) 10: 11: plt.step(recall, precision, color='k', alpha=0.7, where='post') 12: plt.fill_between(recall, precision, step='post', alpha=0.3, color='k') 13: plt.savefig('images/prec-recall-4.png', dpi=300) 14: plt.xlabel('Recall') 15: plt.ylabel('Precision') 16: plt.ylim([0.0, 1.05]) 17: plt.xlim([0.0, 1.0]) 18: 19: plt.title('Precision-Recall curve: Average Precision = {0:0.2f}'.format( 20: average_precision)) 21: 22: fpr, tpr, thresholds = roc_curve(preds['trueLabel'],preds['prediction']) 23: areaUnderROC = auc(fpr, tpr) 24: 25: plt.figure() 26: plt.plot(fpr, tpr, color='r', lw=2, label='ROC curve') 27: plt.plot([0, 1], [0, 1], color='k', lw=2, linestyle='--') 28: plt.xlim([0.0, 1.0]) 29: plt.ylim([0.0, 1.05]) 30: plt.xlabel('False Positive Rate') 31: plt.ylabel('True Positive Rate') 32: plt.title('Receiver operating characteristic: \ 33: Area under the curve = {0:0.2f}'.format(areaUnderROC)) 34: plt.legend(loc="lower right") 35: plt.savefig('images/auROC-4.png', dpi=300)
結果跑不出來,用session跑,除錯有問題,看不到過程
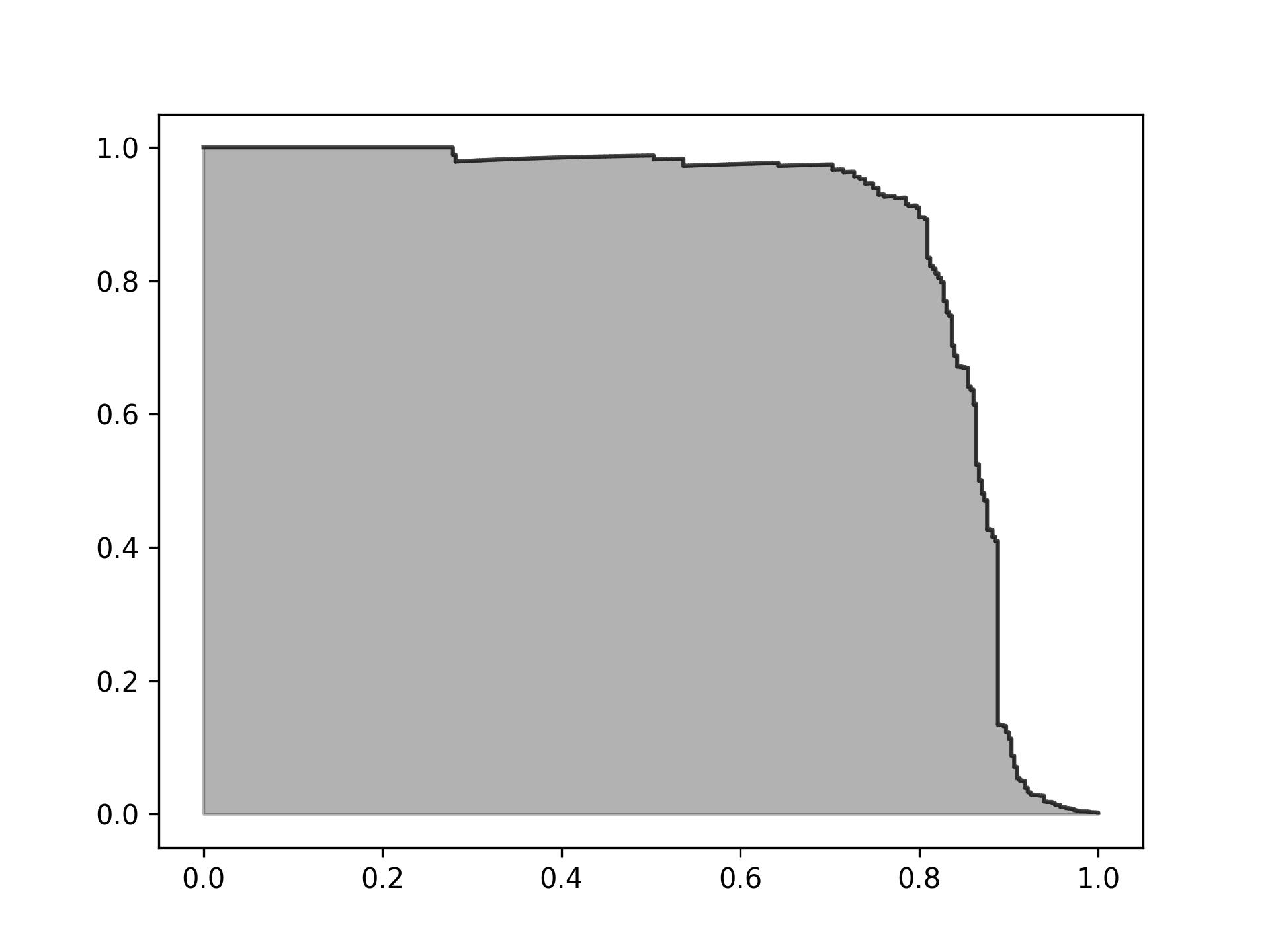
Figure 55: Caption
- 但隨機森林的auROC為0.92,不如Logistic Regression模型的0.97
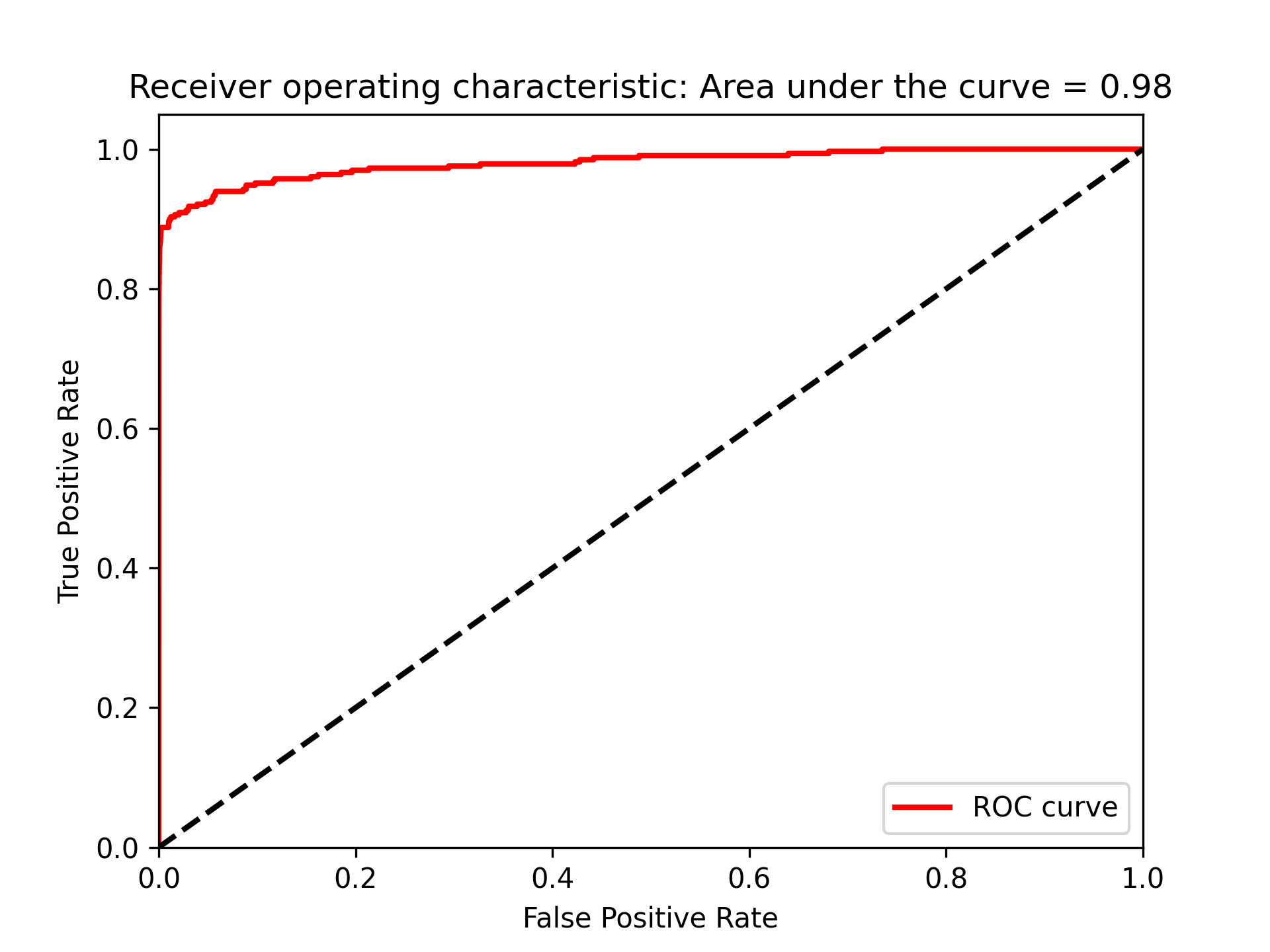
Figure 56: Caption
6.7. Stack
可以將不同家族的模型Stack來改善單一模型的效能,從每個單一模型中取得k-fold交叉驗證的預測結果(第一層預測),將這些預測結果加到原始訓練資料集中,再採用k-fold交叉驗證,利用原始的特徵和第一層預測資料集進行訓練。
6.7.1. 合併
1: # Without XGBoost 2: predictionsBasedOnKFoldsFourModels = pd.DataFrame(data=[],index=y_train.index) 3: predictionsBasedOnKFoldsFourModels = predictionsBasedOnKFoldsFourModels.join( 4: predictionsBasedOnKFoldsLogisticRegression['prediction'].astype(float), \ 5: how='left').join(predictionsBasedOnKFoldsRandomForests['prediction'] \ 6: .astype(float),how='left',rsuffix="2").join( \ 7: predictionsBasedOnKFoldsLightGBMGradientBoosting['prediction'].astype(float), \ 8: how='left',rsuffix="4") 9: predictionsBasedOnKFoldsFourModels.columns = \ 10: ['predsLR','predsRF','predsLightGBM'] 11: 12: predictionsBasedOnKFoldsFourModels = pd.DataFrame(data=[],index=y_train.index) 13: predictionsBasedOnKFoldsFourModels = predictionsBasedOnKFoldsFourModels.join( 14: predictionsBasedOnKFoldsLogisticRegression['prediction'].astype(float), \ 15: how='left').join(predictionsBasedOnKFoldsRandomForests['prediction'] \ 16: .astype(float),how='left',rsuffix="2").join( \ 17: predictionsBasedOnKFoldsXGBoostGradientBoosting['prediction'].astype(float), \ 18: how='left',rsuffix="3").join( \ 19: predictionsBasedOnKFoldsLightGBMGradientBoosting['prediction'].astype(float), \ 20: how='left',rsuffix="4") 21: predictionsBasedOnKFoldsFourModels.columns = \ 22: ['predsLR','predsRF','predsXGB','predsLightGBM'] 23: X_trainWithPredictions = \ 24: X_train.merge(predictionsBasedOnKFoldsFourModels, 25: left_index=True,right_index=True) 26: params_lightGB = { 27: 'task': 'train', 28: 'num_class':1, 29: 'boosting': 'gbdt', 30: 'objective': 'binary', 31: 'metric': 'binary_logloss', 32: 'metric_freq':50, 33: 'is_training_metric':False, 34: 'max_depth':4, 35: 'num_leaves': 31, 36: 'learning_rate': 0.01, 37: 'feature_fraction': 1.0, 38: 'bagging_fraction': 1.0, 39: 'bagging_freq': 0, 40: 'bagging_seed': 2018, 41: 'verbose': -1, 42: 'num_threads':16 43: }
/2024-02-11_15-59-29_2024-02-10_21-14-09.png)